题目内容
已知函数f(x)=lnx-mx+m,m∈R.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若f(x)≤0在(0,+∞)上恒成立,求实数m的取值范围;
(Ⅲ)在(Ⅱ)的条件下,证明:对任意的0<a<b,
≤
-1.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若f(x)≤0在(0,+∞)上恒成立,求实数m的取值范围;
(Ⅲ)在(Ⅱ)的条件下,证明:对任意的0<a<b,
| f(b)-f(a) |
| b-a |
| 1 |
| a |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)求出f(x)的导函数,对参数m分m≤0,m>0两类进行讨论,求出单调区间;
(Ⅱ)f(x)≤0在(0,+∞)上恒成立,即函数f(x)max≤0,结合第(Ⅰ)所求的单调区间,求出函数的最大值;
(Ⅲ)先对要证明的不等式当变形,构造一个形如f(x)的函数,再根据已研究函数的性质,得出要证的结论.
(Ⅱ)f(x)≤0在(0,+∞)上恒成立,即函数f(x)max≤0,结合第(Ⅰ)所求的单调区间,求出函数的最大值;
(Ⅲ)先对要证明的不等式当变形,构造一个形如f(x)的函数,再根据已研究函数的性质,得出要证的结论.
解答:
解:( I)定义域为(0,∞),f′(x)=
-m=
,
当m≤0时,f′(x)=
>0(x>0),∴f(x)在(0,+∞)上单调递增;
当m>0时,令f′(x)=
>0,得0<x<
,∴f(x)在(0,
)上单调递增;
令f′(x)=
<0,得x>
,
∴f(x)在(
,+∞)上单调递减.
∴当m≤0时,f(x)的单调增区间是(0,+∞),无单调减区间;
当m>0时,f(x)的单调增区间是(0,
),单调减区间是(
,+∞).
( II)由( I)知,当m≤0时,f(x)在(0,+∞)上单调递增,
且f(e)=lne-me+m=1+m(1-e)>0,
∴f(x)≤0在(0,+∞)上不恒成立;
当m>0时,由( I)得f(x)max=f(
)=-lnm-1+m,
若使f(x)≤0在(0,+∞)上恒成立,只需-lnm-1+m≤0,
令g(m)=-lnm-1+m,g′(m)=
,
∴当m∈(0,1)时,g'(m)<0,
当m∈(1,+∞)时,g'(m)>0,
∴g(m)min=g(1)=0,∴只有m=1符合题意,
综上得,m=1.
( III)由( II)知m=1,
∴
=
-1=
•
-1,
∵b>a>0,∴
>1,由( II)得,当x∈(0,+∞)时,lnx≤x-1,
∴ln
≤
-1,
∵
>1,∴
≤1,
∵
>0,∴
•
-1≤
-1,
∴
≤
-1.
| 1 |
| x |
| 1-mx |
| x |
当m≤0时,f′(x)=
| 1-mx |
| x |
当m>0时,令f′(x)=
| 1-mx |
| x |
| 1 |
| m |
| 1 |
| m |
令f′(x)=
| 1-mx |
| x |
| 1 |
| m |
∴f(x)在(
| 1 |
| m |
∴当m≤0时,f(x)的单调增区间是(0,+∞),无单调减区间;
当m>0时,f(x)的单调增区间是(0,
| 1 |
| m |
| 1 |
| m |
( II)由( I)知,当m≤0时,f(x)在(0,+∞)上单调递增,
且f(e)=lne-me+m=1+m(1-e)>0,
∴f(x)≤0在(0,+∞)上不恒成立;
当m>0时,由( I)得f(x)max=f(
| 1 |
| m |
若使f(x)≤0在(0,+∞)上恒成立,只需-lnm-1+m≤0,
令g(m)=-lnm-1+m,g′(m)=
| m-1 |
| m |
∴当m∈(0,1)时,g'(m)<0,
当m∈(1,+∞)时,g'(m)>0,
∴g(m)min=g(1)=0,∴只有m=1符合题意,
综上得,m=1.
( III)由( II)知m=1,
∴
| f(b)-f(a) |
| b-a |
| lnb-lna |
| b-a |
| 1 |
| a |
ln
| ||
|
∵b>a>0,∴
| b |
| a |
∴ln
| b |
| a |
| b |
| a |
∵
| b |
| a |
ln
| ||
|
∵
| 1 |
| a |
| 1 |
| a |
ln
| ||
|
| 1 |
| a |
∴
| f(b)-f(a) |
| b-a |
| 1 |
| a |
点评:本题是一道导数的综合题,利用导数求函数的单调区间,这里要对参数进行讨论,解决恒成立问题,构造函数证明不等式,这些都是导数中常考的题型,初学者要多做些这方面的习题.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知全集I={1,2,3,4,5,6},集合M={3,4,5},N={1,2,3,4},则如图中阴影部分表示的集合为( )
已知全集I={1,2,3,4,5,6},集合M={3,4,5},N={1,2,3,4},则如图中阴影部分表示的集合为( )| A、{1,2} |
| B、{1,2,6} |
| C、{1,2,3,4,5} |
| D、{1,2,3,4,6} |
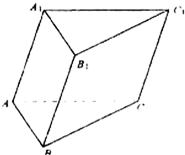 如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为
如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为