题目内容
已知数列{an}和{bn}的通项公式分别为an=3n-19，bn=2n．将{an}与{bn}中的公共项按照从小到大的顺序排列构成一个新数列记为{cn}．
（1）试写出c1，c2，c3，c4的值，并由此归纳数列{cn}的通项公式；
（2）证明你在（1）所猜想的结论．
（1）试写出c1，c2，c3，c4的值，并由此归纳数列{cn}的通项公式；
（2）证明你在（1）所猜想的结论．
考点：二项式定理的应用,归纳推理
专题：点列、递归数列与数学归纳法,二项式定理
分析：（1）按照已知条件写出c1，c2，c3，c4的值，并由此归纳数列{cn}的通项公式；
（2）利用二项式定理直接证明在（1）所猜想的结论．
（2）利用二项式定理直接证明在（1）所猜想的结论．
解答：
解：（1）c1=b1=a7=21，c2=b3=a9=23，c3=b5=a17=25，c4=b7=a48=27，
由此归纳：cn=22n-1．…（4分）
（2）由an=bm，得n=
=
+6，
∴n-6=
，由二项式定理得
∴n-6=
，
∴当m为奇数时，n有整数解，
∴cn=b2n-1=22n-1．…（10分）
由此归纳：cn=22n-1．…（4分）
（2）由an=bm，得n=
| 2m+19 |
| 3 |
| 2m+1 |
| 3 |
∴n-6=
| (3-1)m+1 |
| 3 |
∴n-6=
| ||||||||||
| 3 |
∴当m为奇数时，n有整数解，
∴cn=b2n-1=22n-1．…（10分）
点评：本题考查，二项式定理的应用，归纳推理的应用，基本知识的考查．
练习册系列答案
相关题目
已知全集I={1，2，3，4，5，6}，集合M={3，4，5}，N={1，2，3，4}，则如图中阴影部分表示的集合为（ ）| A、{1，2} |
| B、{1，2，6} |
| C、{1，2，3，4，5} |
| D、{1，2，3，4，6} |
设i为虚数单位，复数z的共轭复数为
，且（
-1）（1+i）=2i，则复数z=（ ）
. |
| z |
. |
| z |
| A、2+i | B、2-i |
| C、-2+i | D、-2-i |
若全集U={1，2，3，4，5，6}，M={1，4}，N={2，3}，则集合{5，6}等于（ ）
| A、M∪N |
| B、M∩N |
| C、（∁UM）∪（∁UN） |
| D、（∁UM）∩（∁UN） |
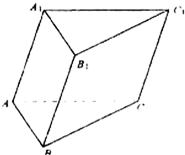如图，用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色，要求四种颜色全都用上，每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色．则不同的涂色方法的种数为