Question

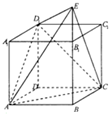如图长方体ABCD-A₁B₁C₁D₁中，底面ABCD是边长为1的正方形，E为BB₁延长线上的一点且满足

BB1

•

B1E

=1．
（Ⅰ）求证：D₁E⊥平面AD₁C；
（Ⅱ）当

B1E

BB1

为何值时，二面角E-AC-D₁的大小为

π

4

．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面垂直的判定

专题：空间角

分析：（Ⅰ）建立空间直角坐标系O-xyz，利用向量法能证明D₁E⊥平面AD₁C．
（Ⅱ）分别求出平面EAC的法向量和平面AD₁C的法向量，利用向量法能求出当

B1E

BB1

=

1

2

时，二面角E-AC-D₁的大小为

π

4

．

解答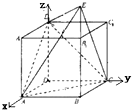： 解：（Ⅰ）如图所示建立空间直角坐标系O-xyz，则A（1，0，0），C（0，1，0），
设DD₁=m，B₁E=n，
由于

BB1

•

B1E

=1，∴mn=1，并且D₁（0，0，m），E（1，1，m+n），…（2分）
∴

D1E

=(1，1，n)，

AD1

=（-1，0，m），

CD1

=（0，-1，m），
∵

D1E

•

AD1

=-1+mn=0，∴D₁E⊥AD₁，
又∵

D1E

•

CD1

=-1+m=0，∴D₁E⊥CD₁，
∵AD₁∩CD₁=D₁，∴D₁E⊥平面AD₁C．…（6分）
（Ⅱ）

AE

=(0，1，m+n)，

CE

=(1，0，m+n)，
设平面EAC的法向量为

t

=(x，y，z)，则

t • AE =y+z(m+n)=0 t • CE =x+z(m+n)=0

，令z=1，
则x=y=-（m+n），∴

t

=(-m-n，-m-n，1)．…（9分）
∵D₁E⊥平面AD₁C，∴平面AD₁C的法向量

D1E

=(1，1，n)，
∵二面角E-AC-D₁的大小为

π

4

．
∴cos

π

4

=|

-2m-2n+n

2(m+n)2+1 • 1+1+n2

|=

2

2

，解得m=

2

，n=

2

2

，…（12分）
∴当

B1E

BB1

=

1

2

时，二面角E-AC-D₁的大小为

π

4

．…（13分）

点评：本题考查直线与平面垂直的证明，考查二面角为

π

4

时线段比值的求法，解题时要认真审题，注意向量法的合理运用．