题目内容
20.一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的北偏东45°,则货轮的速度为( )| A. | $20(\sqrt{3}+\sqrt{6})$海里/时 | B. | $20(\sqrt{6}-\sqrt{3})$海里/时 | C. | $20(\sqrt{2}+\sqrt{6})$海里/时 | D. | $20(\sqrt{6}-\sqrt{2})$海里/时 |
分析 根据题意画出相应的图形,在三角形PMN中,根据sin∠MPN与sin∠PNM的值,以及PM的长,利用正弦定理求出MN的长,除以时间即可确定出速度.
解答  解:由题意知PM=20海里,∠PMB=15°,∠BMN=30°,∠PNC=45°,
解:由题意知PM=20海里,∠PMB=15°,∠BMN=30°,∠PNC=45°,
∴∠NMP=45°,∠MNA=90°-∠BMN=60°,
∴∠PNM=105°,
∴∠MPN=30°,
∵sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=$\frac{\sqrt{2}+\sqrt{6}}{4}$,
∴在△MNP中利用正弦定理可得MN=$\frac{20sin30°}{sin105°}$=10($\sqrt{6}$-$\sqrt{2}$)海里,
∴货轮航行的速度v=$\frac{10(\sqrt{6}-\sqrt{2})}{\frac{1}{2}}$=20($\sqrt{6}$-$\sqrt{2}$))海里/小时.
故选D.
点评 此题考查了正弦定理在解三角形中的应用,解决实际问题的关键是要把实际问题转化为数学问题,然后利用数学知识进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列函数能用二分法求零点的是( )
| A. | f(x)=x2 | B. | f(x)=$\sqrt{-{x^2}+1}$ | C. | f(x)=ln(x+2)2 | D. | f(x)=$\frac{1}{{|{{2^x}-3}|}}$ |
11.直线y=kx+3被圆(x-2)2+(y-3)2=4截得的弦长为$2\sqrt{3}$,则直线的倾斜角为( )
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $-\frac{π}{3}$或$\frac{π}{3}$ | C. | $-\frac{π}{6}$或$\frac{π}{6}$ | D. | $\frac{π}{6}$ |
10.p:log2a>0是q:$\frac{1}{a}$<1 的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
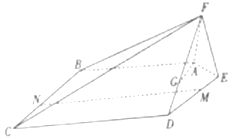 如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.