题目内容
10.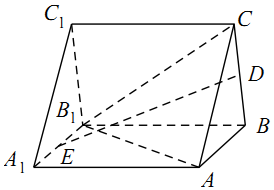 在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.(Ⅰ)求证:DE?平面ACC1A1;
(Ⅱ)若AB⊥BC,AB=BC,∠ACB1=60°,求直线BC与平面AB1C所成角的正切值.
分析 (Ⅰ)取AB中点F,连接DF,EF证明以DF∥AC,推出DF∥平面ACC1A1.证明EF∥AA1,推出EF∥平面ACC1A1,然后证明DE?平面ACC1A1.
(Ⅱ)证明△AB1C为正三角形,推出BB1=AB.取AB1的中点O,连接BO,CO,说明∠BCO即为直线BC与平面AB1C所成角,在RtBCO中,求解即可.
解答 解:(Ⅰ)取AB中点F,连接DF,EF.…(1分)
在△ABC中,因为D,F分别为BC,AB的中点,所以DF∥AC,DF?平面ACC1A1,AC?平面ACC1A1,
所以DF∥平面ACC1A1.…(3分)
在矩形ABB1A1中,因为E,F分别为B1A1,AB的中点,
所以EF∥AA1,EF?平面ACC1A1,AA1?平面ACC1A1,所以EF∥平面ACC1A1.…(4分)
因为DF∩EF=F,所以平面DEF∥平面ACC1A1.…(5分)
因为DE?平面ACC1A1.…(6分)
(Ⅱ)因为三棱柱ABC-A1B1C1为直三棱柱,所以BC⊥BB1,
又AB⊥BC,AB∩BB1=B,所以BC⊥平面ABB1A1.…(7分)
因为AB=BC,BB1=BB1,所以AB1=CB1,
又∠ACB1=60°,所以△AB1C为正三角形,
所以AB1=$\sqrt{A{B}^{2}+B{{B}_{1}}^{2}}$=AC=$\sqrt{2}AB$,所以BB1=AB.…(8分)
取AB1的中点O,连接BO,CO,所以AB1⊥BO,AB1⊥CO,所以AB1⊥平面BCD,
所以平面AB1C⊥平面BCD,点B在平面AB1C上的射影在CO上,
所以∠BCO即为直线BC与平面AB1C所成角.…(10分)
在RtBCO中,BO=$\frac{\sqrt{2}}{2}AB=\frac{\sqrt{2}}{2}BC$,所以tan∠BCO$\frac{BO}{BC}$=$\frac{\sqrt{2}}{2}$.…(12分)
点评 本题考查直线与平面市场价的求法,直线与平面平行于垂直的判定定理的应用,考查空间想象能力以及计算能力.

| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{32\sqrt{3}}{3}$ | D. | $\frac{64\sqrt{3}}{3}$ |
| A. | 若x>1,则?y∈(-∞,1),xy≠1 | B. | 若x=sinθcosθ,则?θ∈(0,π),x≠$\frac{1}{2}$ | ||
| C. | 若x>1,则?y∈(-∞,1),xy=1 | D. | 若x=sinθcosθ,则?θ∈(0,π),x=1 |
| A. | f(x)=$\frac{1}{x-1}$,g(x)=$\frac{x+1}{{x}^{2}-1}$ | B. | f(x)=|x+1|,g(x)=$\sqrt{{x}^{2}+2x+1}$ | ||
| C. | f(x)=x0,g(x)=1 | D. | f(x)=3x+2(x≥0),g(x)=2+3x |
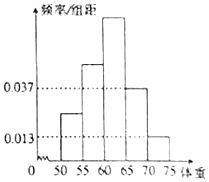 为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.