题目内容
5.使sinα=m-2有意义的m的取值范围是[1,3].分析 根据正弦函数的有界性进行求解即可.
解答 解:∵-1≤sinα≤1,
∴由sinα=m-2得-1≤m-2≤1,
得1≤m≤3,
故答案为:[1,3].
点评 本题主要考查三角函数的图象和性质,利用正弦函数的有界性是解决本题的关键.比较基础.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10.p:log2a>0是q:$\frac{1}{a}$<1 的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.不等式kx2-kx+1>0对一切实数x均成立,则k的取值范围是( )
| A. | 0<k<4 | B. | 0≤k<4 | C. | 0<k≤4 | D. | 0≤k≤4 |
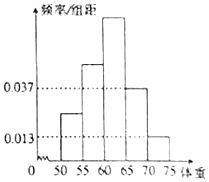 为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.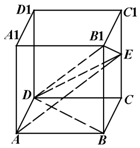 在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.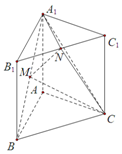 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.