题目内容
在△ABC中,已知向量
=(sinA,1),
=(cosA,
),且
∥
,其中A∈(0,
).
(1)若sin(ω-A)=
,0<ω<
,求cosω的值;
(2)若BC=2
,AC+AB=4,求△ABC的面积.
| a |
| b |
| 3 |
| a |
| b |
| π |
| 2 |
(1)若sin(ω-A)=
| 3 |
| 5 |
| π |
| 2 |
(2)若BC=2
| 3 |
考点:两角和与差的正弦函数,三角形的面积公式
专题:计算题,三角函数的求值,平面向量及应用
分析:(Ⅰ)由
∥
,得tanA=
,由sin(ω-A)=
,可得sinω=
,由0<ω<
,得sinω的值,从而有
=
,可解得cosω的值;
(2)由余弦定理可得AB•AC=
,即可求△ABC的面积.
| a |
| b |
| ||
| 3 |
| 3 |
| 5 |
| ||
|
| π |
| 2 |
| ||
|
| 1-cos2ω |
(2)由余弦定理可得AB•AC=
| 4 | ||
2+
|
解答:
解:(Ⅰ)由
∥
,得cosA-
sinA=0,化为tanA=
,
∵A∈(0,
).
∴A=
∵sin(ω-A)=
,可得sinω=
,
∵0<ω<
,∴sinω=
,
∴
=
,整理可得100cos2ω+60cosω-39=0,解得cosω=
(舍去)或
;
(2)∵BC=2
,AC+AB=4,A=
∴由余弦定理可得:12=AB2+AC2-2•AB•AC•sinA=(AB+AC)2-(2+
)AB•AC=16-(2+
)AB•AC
∴可解得:AB•AC=
∴S△ABC=
•AB•AC•sinA=
×
=2-
.
| a |
| b |
| 3 |
| ||
| 3 |
∵A∈(0,
| π |
| 2 |
∴A=
| π |
| 6 |
∵sin(ω-A)=
| 3 |
| 5 |
| ||
|
∵0<ω<
| π |
| 2 |
| 1-cos2ω |
∴
| ||
|
| 1-cos2ω |
-3-4
| ||
| 10 |
4
| ||
| 10 |
(2)∵BC=2
| 3 |
| π |
| 6 |
∴由余弦定理可得:12=AB2+AC2-2•AB•AC•sinA=(AB+AC)2-(2+
| 3 |
| 3 |
∴可解得:AB•AC=
| 4 | ||
2+
|
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 4 |
| 4 | ||
2+
|
| 3 |
点评:本题主要考察了两角和与差的正弦函数,三角形的面积公式,本题计算量较大,要求解题时认真细心,属于基本知识的考查.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
sin(α-
)=( )
| π |
| 2 |
| A、sinα | B、-sinα |
| C、cosα | D、-cosα |
双曲线与椭圆
+
=1有相同的焦点,且离心率为
,则双曲线方程为( )
| x2 |
| 16 |
| y2 |
| 64 |
| 2 |
| A、x2-y2=96 |
| B、y2-x2=100 |
| C、x2-y2=80 |
| D、y2-x2=24 |
已知函数y=Asin(ωx+φ)+m的最大值为4,最小值为-2,两条对称轴间的最短距离为
,直线x=
是其图象的一条对称轴,则符合条件的一个解析式是( )
| π |
| 2 |
| π |
| 6 |
A、y=6sin(2x+
| ||
B、y=6sin(4x+
| ||
C、y=3sin(4x-
| ||
D、y=3sin(2x-
|
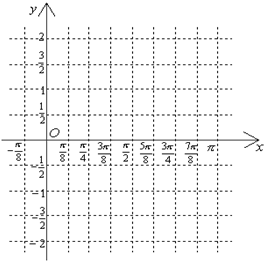 已知曲线f(x)=Asin(ωx+ϕ)+B(A>0,ω>0,|φ|<
已知曲线f(x)=Asin(ωx+ϕ)+B(A>0,ω>0,|φ|<