题目内容
y=ax(a>0,a≠1)是减函数,则函数f(x)=loga(x2+2x-3)的增区间是 .
考点:复合函数的单调性
专题:函数的性质及应用
分析:由题意可得0<a<1,令t=x2+2x-3>0,求得f(x)的定义域为{x|x<-3,x>1},函数f(x)=logat,本题即求函数t在{x|x<-3,x>1}上的减区间.
再利用二次函数的性质可得结论.
再利用二次函数的性质可得结论.
解答:
解:由y=ax(a>0,a≠1)是减函数,可得0<a<1,令t=x2+2x-3>0,求得f(x)的定义域为{x|x<-3,x>1},
且函数f(x)=logat,
故本题即求函数t在{x|x<-3,x>1}上的减区间.
再利用二次函数的性质可得函数t在{x|x<-3,x>1}上的减区间为(-∞,-3),
故答案为:(-∞,-3).
且函数f(x)=logat,
故本题即求函数t在{x|x<-3,x>1}上的减区间.
再利用二次函数的性质可得函数t在{x|x<-3,x>1}上的减区间为(-∞,-3),
故答案为:(-∞,-3).
点评:本题主要考查复合函数的单调性,对数函数、二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
,把函数g(x)=f(x)-
x的偶数零点按从小到大的顺序排列成一个数列,该数列的前n项的和Sn,则S10=( )
|
| 1 |
| 2 |
| A、45 | B、55 | C、90 | D、110 |
阅读如图的程序框图,若输入的n是100,则输出的变量S的值是( )


| A、5 049 |
| B、5 050 |
| C、5 051 |
| D、5 052 |
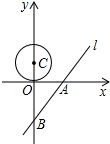 如图所示,已知直线l的解析式是y=
如图所示,已知直线l的解析式是y= 如图,在直三棱柱ABC-A1B1C1中,AC=AB=AA1=4,∠BAC=90°,点D是棱B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=AB=AA1=4,∠BAC=90°,点D是棱B1C1的中点.