题目内容
若1+sinθ
+cosθ
=0成立,则角θ不可能是 .
| sin2θ |
| cos2θ |
考点:三角函数的化简求值
专题:三角函数的求值
分析:由已知化简可得sinθ|sinθ|+cosθ|cosθ|=-1,分情况讨论即可.
解答:
解:∵1+sinθ
+cosθ
=0
∴1+sinθ|sinθ|+cosθ|cosθ|=0
∴sinθ|sinθ|+cosθ|cosθ|=-1
若θ是第一象限,则sinθ>0,cosθ>0,不成立
若θ是第二象限,则sinθ>0,cosθ<0,虽然cosθ|cosθ|<0,但cosθ|cosθ|≥-1,不成立
同理,θ是第四象限也不成立.
故角θ不可能是第1,2,4象限角.
故答案为:第1,2,4象限角.
| sin2θ |
| cos2θ |
∴1+sinθ|sinθ|+cosθ|cosθ|=0
∴sinθ|sinθ|+cosθ|cosθ|=-1
若θ是第一象限,则sinθ>0,cosθ>0,不成立
若θ是第二象限,则sinθ>0,cosθ<0,虽然cosθ|cosθ|<0,但cosθ|cosθ|≥-1,不成立
同理,θ是第四象限也不成立.
故角θ不可能是第1,2,4象限角.
故答案为:第1,2,4象限角.
点评:本题主要考察了三角函数的化简求值,属于基本知识的考查.

练习册系列答案
相关题目
集合A={x||x-1|<2},B={x|2-x-x2>0},则A∩B=( )
| A、(-2,3) |
| B、(-1,1) |
| C、(1,3) |
| D、(-1,2) |
已知不同的三点A、B、C满足
=λ
(λ∈R,λ≠0),使得关于x的方程x2
+x
-
=
有解(点O不在直线AB上),则此方程在实数范围内的解集为( )
| AB |
| BC |
| OA |
| OB |
| OC |
| 0 |
| A、∅ | ||||||||
| B、{-1,0} | ||||||||
| C、{-1} | ||||||||
D、{
|
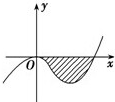 已知函数f(x)=x3+ax2+bx+c(a、b、c∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成的区域(图中阴影部分)的面积为
已知函数f(x)=x3+ax2+bx+c(a、b、c∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成的区域(图中阴影部分)的面积为