题目内容
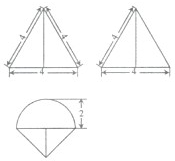
某简单组合体的三视图如图所示,则该组合体的体积为( )

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:组合几何体的面积、体积问题
专题:空间位置关系与距离
分析:几何体是一个简单的空间组合体,前面是半个圆锥,圆锥的底面是半径为2的圆,母线长是6,后面是一个三棱锥,三棱锥的底边长是4、高为2的等腰三角形,三棱锥的高是2
,求出两个几何体的体积,求和得到结果.
| 3 |
解答:
解:由三视图知,几何体是一个简单的空间组合体,
前面是半个圆锥,圆锥的底面是半径为2的圆,母线长是4,
∴根据勾股定理知圆锥的高是
=2
,
∴半个圆锥的体积是
×
×π×22×2
=
,
后面是一个三棱锥,三棱锥的底是边长为4、高为2的等腰三角形,三棱锥的高是2
,
∴三棱锥的体积是
×
×4×2×2
=
,
∴几何体的体积是
+
=
(π+2).
故选:B.
前面是半个圆锥,圆锥的底面是半径为2的圆,母线长是4,
∴根据勾股定理知圆锥的高是
| 42-22 |
| 3 |
∴半个圆锥的体积是
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
后面是一个三棱锥,三棱锥的底是边长为4、高为2的等腰三角形,三棱锥的高是2
| 3 |
∴三棱锥的体积是
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
8
| ||
| 3 |
∴几何体的体积是
4
| ||
| 3 |
8
| ||
| 3 |
4
| ||
| 3 |
故选:B.
点评:本题考查由三视图求几何体的体积,考查由三视图还原几何体直观图,考查锥体的体积公式,本题是中档题.

练习册系列答案
相关题目
在一次防恐演习中,某射手击中目标的概率为0.8,每次射击的结果相互独立,现射击99次,则他最有可能射中目标( )次.
| A、99 | B、80 |
| C、79或80 | D、79 |
若复数x满足x+i=
,则复数x的模为( )
| 2-i |
| i |
A、
| ||
| B、10 | ||
| C、4 | ||
D、
|
已知函数f(x)(x∈R)的图象上任一点(x0,y0)处切线的方程为:y-y0=(x0-2)( x0-1)(x-x0),那么函数f(x)的单调减区间是( )
| A、(1,2) |
| B、(-∞,1] |
| C、[2,+∞) |
| D、(-∞,-1) |
已知集合A={x|y=
},B={y|y=2x,x∈R},则A∩B=( )
| x-x2 |
| A、[0,1] |
| B、(0,1) |
| C、(0,1] |
| D、[0,1) |
已知
sin(π-2x)-1=cos2x(0<x<π),则tan2x的值是( )
| 1 |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|