题目内容
空间四边形ABCD中,若AB=BC=CD=DA=BD=1,则AC的取值范围是 .
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:运用图形得|
|=|
+
|,再根据向量求解.
| AC |
| AO |
| OB |
解答:
 解:0为BD中点,
解:0为BD中点,
∵AB=BC=CD=DA=BD=1,
∴|OA|=|OB|=
,
|
|=|
+
|=
=
,θ∈(0°,180°]
∴AC的取值范围是(0,
]
故答案为:(0,
]
 解:0为BD中点,
解:0为BD中点,∵AB=BC=CD=DA=BD=1,
∴|OA|=|OB|=
| ||
| 2 |
|
| AC |
| AO |
| OB |
(
|
|
∴AC的取值范围是(0,
| 3 |
故答案为:(0,
| 3 |
点评:本题考查了向量的运用求解距离,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
是R上的增函数,那么实数a的取值范围为( )
|
A、(
| ||
| B、(1,+∞) | ||
| C、[2,+∞) | ||
| D、(1,2) |
已知坐标原点O在圆x2+y2-x+y+m=0外,则m的取值范围是( )
A、0<m<
| ||
B、m<
| ||
C、m≤
| ||
| D、m>0 |
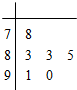 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:①中位数为84;
②众数为85;
③平均数为85;
④极差为12.
其中,正确说法的序号是( )
| A、①② | B、③④ | C、②④ | D、①③ |
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图示,则下列说法不正确的是( )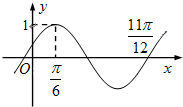
| π |
| 2 |

| A、ω=2 | ||||
B、f(x)的图象关于点(
| ||||
C、k(x)=f(
| ||||
| D、已知函数g(x)=cos(ξx+η)图象与f(x)的对称轴完全相同,则ξ=2 |
把一枚硬币任意抛掷三次,事件A=“至少一次出现反面”,事件B=“恰有一次出现正面”,则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|