题目内容
4.若函数f(x)在区间[m,n]上为增函数,则f(x)在[m,n]上( )| A. | 只有一个零点 | B. | 至少有一个零点 | C. | 至多有一个零点 | D. | 没有零点 |
分析 若函数f(x)在区间[m,n]上有两个零点,则函数f(x)在区间[m,n]上不可能是单调函数,从而判断.
解答 解:若函数f(x)在区间[m,n]上有两个零点,
则函数f(x)在区间[m,n]上不可能是单调函数,
故f(x)在[m,n]上至多有一个零点,
故选:C.
点评 本题考查了函数的单调性及零点的判定定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.在△ABC中,a2+b2-c2=ab,则cosC=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
16.三棱锥P-ABC三条侧棱两两垂直,三条侧棱长分别为1,$\sqrt{5}$,$\sqrt{10}$,则该三棱锥的外接球体积为( )
| A. | $\frac{32}{3}$π | B. | $\frac{16}{3}$π | C. | 32π | D. | 16π |
13.若函数f(x)同时满足以下三个性质:①f(x)的最小正周期为π;②对任意的x∈R,都有f(x-$\frac{π}{4}$)+f(-x)=0;③f(x)在($\frac{π}{4}$,$\frac{π}{2}$)上是减函数,则f(x)的解析式可能是( )
| A. | f(x)=sin2x+cos2x | B. | f(x)=sin2x | C. | f(x)=tan(x+$\frac{π}{8}$) | D. | f(x)=cos2x |
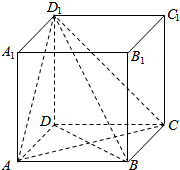 如图,在正方形ABCD-A′B′C′D′,AB=1,
如图,在正方形ABCD-A′B′C′D′,AB=1, 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F,短轴的两个端点分别为A,B,且|AB|=2,△ABF为等边三角形.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F,短轴的两个端点分别为A,B,且|AB|=2,△ABF为等边三角形.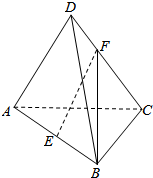 如图,在空间四边形ABCD中,E是线段AB的中点.
如图,在空间四边形ABCD中,E是线段AB的中点.