题目内容
12．
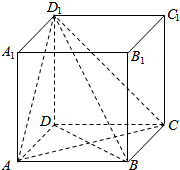如图，在正方形ABCD-A′B′C′D′，AB=1，（1）求异面直线AD′与DC′所成的角；
（2）求证：A′B∥平面ACD′；
（3）求VA-CDD′．
分析 （1）连接BC′，则BC′∥AD′，∠BC′D是异面直线AD′与DC′所成的角；
（2）证明四边形A′BCD′为平行四边形．推出A′B∥CD’，然后证明A′B∥平面ACD′，
（3）直接利用体积公式，即可得出结论．
解答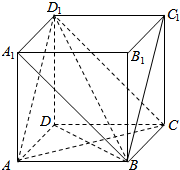 
（1）解：连接BC′，则BC′∥AD′，
∴∠BC′D是异面直线AD′与DC′所成的角，
∵BD=DC′=C′B，
∴∠BC′D=60°，
∴异面直线AD′与DC′所成的角为60°；
（2）证明：∵A′D∥′BC，且A′D=B′C
∴四边形A′BCD′为平行四边形．
∴A′B∥CD′，
又∵A′B?平面ACD′，CD′?平面ACD′
∴A′B∥平面ACD′；
（3）解：VA-CDD′=$\frac{1}{3}$S△CDD′•AD=$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{1}{6}$．
点评 本题考查直线与平面平行，异面直线AD′与DC′所成的角，三棱锥体积的计算，考查空间想象能力，逻辑推理能力．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
2．△ABC的三内角A，B，C所对边长分别是a，b，c，设向量$\overrightarrow n=（\sqrt{3}a+c，sinB-sinA）$，$\overrightarrow m=（a+b，sinC）$，若$\overrightarrow m∥\overrightarrow n$，则角B的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{5π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
20．已知函数f（x）在[0，+∞）上递增，$f（\frac{1}{3}）=0$，已知g（x）=-f（|x|），满足$g（{log_{\frac{1}{8}}}x）＞0$的x的取值范围是（ ）
| A． | （0，+∞） | B． | $（0，\frac{1}{2}）∪（2，+∞）$ | C． | $（0，\frac{1}{8}）∪（\frac{1}{2}，2）$ | D． | $（\frac{1}{2}，2）$ |
7．圆C1：x2+y2+2x+2y-2=0与圆C2：x2+y2-4x-2y+1=0（ ）
| A． | 外离 | B． | 外切 | C． | 相交 | D． | 内切 |
4．若函数f（x）在区间[m，n]上为增函数，则f（x）在[m，n]上（ ）
| A． | 只有一个零点 | B． | 至少有一个零点 | C． | 至多有一个零点 | D． | 没有零点 |
