题目内容
17.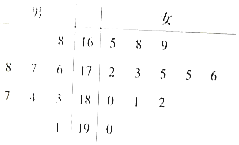 某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.
(Ⅰ)求8名男志愿者的平均身高和12名女志愿者身高的中位数;
(Ⅱ)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
分析 (Ⅰ)利用茎叶图能求出8名男志愿者的平均身高和12名女志愿者身高的中位数.
(Ⅱ)根据茎叶图,有“高个子”8人,“非高个子”12人,用分层抽样的方法,选中的“高个子”2人,“非高个子”3人,从这五个人选出两人,利用列举法能求出至少有一个是“高个子”的概率.
解答 解:(Ⅰ)8名男志愿者的平均身高为:
$\frac{168+176+177+178+183+184+187+191}{8}=180.5$.…(3分)
12名女志愿者身高的中位数为175.…(6分)
(Ⅱ)根据茎叶图,有“高个子”8人,“非高个子”12人,
用分层抽样的方法,每个人被抽中的概率是$\frac{5}{20}=\frac{1}{4}$.
所以选中的“高个子”有$8×\frac{1}{4}=2$人,设这两个人为A,B;
“非高个子”有$12×\frac{1}{4}=3$人,设这三个人为C,D,E.
从这五个人A,B,C,D,E中选出两人共有:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),
(B,E),(C,D),(C,E),(D,E)十种不同方法;…(10分)
其中至少有一人是“高个子”的选法有:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E)七种.
因此,至少有一个是“高个子”的概率是$\frac{7}{10}$.…(12分)
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
7.设m、n是两条不同的直线,α、β是两个不同的平面,则( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥n,n⊥α,则m⊥α | C. | 若m∥α,m∥β,则α∥β | D. | 若m∥α,α⊥β,则m⊥β |
5.函数$f(x)={(6-x-{x^2})^{\frac{3}{2}}}$的单调递减区间为( )
| A. | $[{-\frac{1}{2},2}]$ | B. | $[{-3,-\frac{1}{2}}]$ | C. | $[-\frac{1}{2},+∞)$ | D. | $(-∞,-\frac{1}{2}]$ |
2.已知向量$\overrightarrow a=({\frac{1}{2},sinα})$,$\overrightarrow b=({sinα,1})$,若$\overrightarrow a∥\overrightarrow b$,则锐角α为( )
| A. | 30° | B. | 60° | C. | 45° | D. | 75° |
7.某名学生默写英语单词“bookkeeper(会计)”,他记得这个单词是由3个“e”,2个“o”,2个“k”,b,p,r各一个组成,2个“o”相邻,3个“e”恰有两个相邻,o,e都不在首位,他按此条件任意写出一个字母组合,则他写对这个单词的概率为( )
| A. | $\frac{1}{9600}$ | B. | $\frac{1}{18000}$ | C. | $\frac{1}{4500}$ | D. | $\frac{1}{10800}$ |