题目内容
7.某名学生默写英语单词“bookkeeper(会计)”,他记得这个单词是由3个“e”,2个“o”,2个“k”,b,p,r各一个组成,2个“o”相邻,3个“e”恰有两个相邻,o,e都不在首位,他按此条件任意写出一个字母组合,则他写对这个单词的概率为( )| A. | $\frac{1}{9600}$ | B. | $\frac{1}{18000}$ | C. | $\frac{1}{4500}$ | D. | $\frac{1}{10800}$ |
分析 由排列组合知识求出基本事件总数n=${A}_{5}^{5}{C}_{4}^{1}{A}_{5}^{2}$=9600,由此能求出他写对这个单词的概率.
解答 解:某名学生默写英语单词“bookkeeper(会计)”,他记得这个单词是由3个“e”,2个“o”,2个“k”,b,p,r各一个组成,
2个“o”相邻,3个“e”恰有两个相邻,o,e都不在首位,他按此条件任意写出一个字母组合,
基本事件总数n=${A}_{5}^{5}{C}_{4}^{1}{A}_{5}^{2}$=9600,
∴他按此条件任意写出一个字母组合,则他写对这个单词的概率为p=$\frac{1}{9600}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知x,y满足线性约束条件$\left\{\begin{array}{l}y-x≤3\\ x+y≤5\\ y≥λ\end{array}\right.$,若z=x+4y的最大值与最小值之差为5,则实数λ的值为( )
| A. | 3 | B. | $\frac{7}{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
2.为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如表:
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”?
参考公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(n=a+b+c+d).
附表:
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为X,求X的数学期望E(X).
| 与教育有关 | 与教育无关 | 合计 | |
| 男 | 30 | 10 | 40 |
| 女 | 35 | 5 | 40 |
| 合计 | 65 | 15 | 80 |
参考公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(n=a+b+c+d).
附表:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为X,求X的数学期望E(X).
12.已知集合A={x∈Z|(x+2)(x-1)<0},B={-2,-1},那么A∪B等于( )
| A. | {-1} | B. | {-2,-1} | C. | {-2,-1,0} | D. | {-2,-1,0,1} |
16.设集合M={x|x=2k+1,k∈Z},N={x|x=k+2,k∈Z},则.( )
| A. | M=N | B. | M?N | C. | N?M | D. | M∩N=∅ |
17.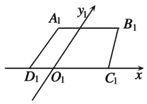 如图,梯形A1B1C1D1是一平面图形ABCD的直观图(斜二测),若AD∥Oy,AB∥CD,A1B1=$\frac{3}{4}{C_1}{D_1}=3,{A_1}{D_1}$=1,则原平面图形ABCD的面积是( )
如图,梯形A1B1C1D1是一平面图形ABCD的直观图(斜二测),若AD∥Oy,AB∥CD,A1B1=$\frac{3}{4}{C_1}{D_1}=3,{A_1}{D_1}$=1,则原平面图形ABCD的面积是( )
 如图,梯形A1B1C1D1是一平面图形ABCD的直观图(斜二测),若AD∥Oy,AB∥CD,A1B1=$\frac{3}{4}{C_1}{D_1}=3,{A_1}{D_1}$=1,则原平面图形ABCD的面积是( )
如图,梯形A1B1C1D1是一平面图形ABCD的直观图(斜二测),若AD∥Oy,AB∥CD,A1B1=$\frac{3}{4}{C_1}{D_1}=3,{A_1}{D_1}$=1,则原平面图形ABCD的面积是( )| A. | 14. | B. | 7 | C. | $14\sqrt{2}$ | D. | $7\sqrt{2}$ |
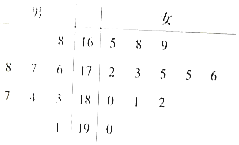 某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)