题目内容
7.设m、n是两条不同的直线,α、β是两个不同的平面,则( )| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥n,n⊥α,则m⊥α | C. | 若m∥α,m∥β,则α∥β | D. | 若m∥α,α⊥β,则m⊥β |
分析 A.由已知可得:m∥n或相交或为异面直线;
B.利用线面垂直的性质定理即可判断出正误;
C.由m∥α,m∥β,则α∥β或相交,即可判断出正误;
D.由已知可得m与β相交或m?β,即可判断出正误.
解答 解:A.由m∥α,n∥α,则m∥n或相交或为异面直线;
B.m∥n,n⊥α,利用线面垂直的性质定理即可得出m⊥α,因此正确;
C.∵m∥α,m∥β,则α∥β或相交,因此不正确;
D.∵m∥α,α⊥β,则m与β相交或m?β,不正确.
故选:B.
点评 本题考查了空间位置关系、线面垂直与平行的性质定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.函数f(x)=($\frac{1}{2}$)x-x-2的零点所在的区间为( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
18.某四棱锥的三视图如图所示,该四棱锥的表面积为( )


| A. | $1+\sqrt{2}$ | B. | 3 | C. | $2+\sqrt{2}$ | D. | 4 |
15.任取一个3位正整数n,则对数log2n是一个正整数的概率为( )
| A. | $\frac{1}{225}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{450}$ | D. | 以上全不对 |
2.如图,已知PA垂直于平行四边形ABCD所在平面,若PC⊥BD,则平行四边形ABCD一定是( )
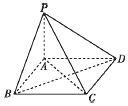

| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 非上述三种图形 |
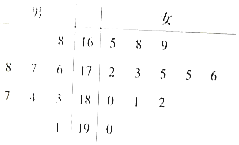 某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)