题目内容
12.已知数列{an}满足${a_n}+{a_{n-1}}={({-1})^{\frac{{n({n+1})}}{2}}}n,{S_n}$是其前n项和,若S2017=-1007-b,且a1b>0,则$\frac{1}{a_1}+\frac{2}{b}$的最小值为3+2$\sqrt{2}$.分析 由已知得:a3+a2=3,a5+a4=-5,…a2017+a2016=-2017,把以上各式相加得:S2017-a1=-1008,可得a1+b=1,又a1b>0,a1,b>0.再利用“乘1法”与基本不等式性质即可得出.
解答 解:由已知得:a3+a2=3,a5+a4=-5,…a2017+a2016=-2017,
把以上各式相加得:S2017-a1=-1008,
即:a1-1008=-1007-b,
∴a1+b=1,又a1b>0,
∴a1,b>0.
则$\frac{1}{a_1}+\frac{2}{b}$=(a1+b)$(\frac{1}{{a}_{1}}+\frac{2}{b})$=3+$\frac{b}{{a}_{1}}$+$\frac{2{a}_{1}}{b}$≥3+$2\sqrt{\frac{b}{{a}_{1}}•\frac{2{a}_{1}}{b}}$=3+2$\sqrt{2}$,当且仅当b=$\sqrt{2}$a1=2-$\sqrt{2}$时取等号.
故答案为:$3+2\sqrt{2}$.
点评 本题考查了“累加求和”、“乘1法”与基本不等式性质,考查了分类讨论方法、推理能力与就计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.如图,已知PA垂直于平行四边形ABCD所在平面,若PC⊥BD,则平行四边形ABCD一定是( )
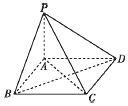

| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 非上述三种图形 |
20.解α的终边过点P(4,-3),则cosα的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | 4 | D. | -3 |
1.图中曲线的方程可以是( )
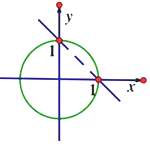

| A. | (x+y-1)•(x2+y2-1)=0 | B. | $\sqrt{x+y-1}•({x^2}+{y^2}-1)=0$ | ||
| C. | $(x+y-1)•\sqrt{{x^2}+{y^2}-1}=0$ | D. | $\sqrt{x+y-1}•\sqrt{{x^2}+{y^2}-1}=0$ |
2.为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如表:
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”?
参考公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(n=a+b+c+d).
附表:
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为X,求X的数学期望E(X).
| 与教育有关 | 与教育无关 | 合计 | |
| 男 | 30 | 10 | 40 |
| 女 | 35 | 5 | 40 |
| 合计 | 65 | 15 | 80 |
参考公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(n=a+b+c+d).
附表:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为X,求X的数学期望E(X).
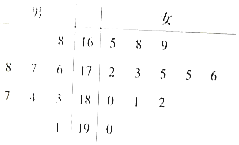 某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)