题目内容

2．已知向量$\overrightarrow a=（{\frac{1}{2}，sinα}）$，$\overrightarrow b=（{sinα，1}）$，若$\overrightarrow a∥\overrightarrow b$，则锐角α为（　　）
A．30°B．60°C．45°D．75°

分析 根据两个向量平行，交叉相乘差为0，易得到一个三角方程，根据α为锐角，我们易求出满足条件的值

解答 解：向量$\overrightarrow a=（{\frac{1}{2}，sinα}）$，$\overrightarrow b=（{sinα，1}）$，$\overrightarrow a∥\overrightarrow b$，
∴$\frac{1}{2}$=sin2a
∴sinα=±$\frac{\sqrt{2}}{2}$，
又∵α为锐角，
∴α=45°，
故选：C．

点评 本题考查的知识点是平面向量共线（平行）的坐标表示，及三角函数的化简求值，其中根据两个向量平行，交叉相乘差为0，构造三角方程是解答本题的关键．

练习册系列答案
相关题目
12．若函数f（x+1）=2x2+1，则函数f（x）=2x2-4x+3．
13．已知$A=\left\{{x|\frac{1}{8}＜{2^{-x}}＜\frac{1}{2}}\right\}\;，\;\;B=\left\{{x|{{log}_2}（{x-2}）＜1}\right\}$，则A∩B={x|2＜x＜3}．
10．“x＞1”是“$\frac{1}{x}＜1$”成立的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
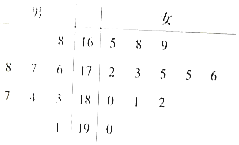17．某校开展运动会，招募了8名男志愿者和12名女志愿者，将这20名志愿者的身高编成如下茎叶图（单位：cm）
若身高在180cm以上（包括180cm）定义为“高个子”，身高在180cm以下（不包括180cm）定义为“非高个子”．
（Ⅰ）求8名男志愿者的平均身高和12名女志愿者身高的中位数；
（Ⅱ）如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人，再从这5人中选2人，那么至少有一人是“高个子”的概率是多少？
7．△ABC的内角A，B，C的对边分别为a，b，c，已知bcosC=（2a-c）cosB．
（Ⅰ）求B；
（Ⅱ）若c=2，b=3，求△ABC的面积．
14．若（2+x）n的二项展开式中，所有二项式的系数和为256，则正整数n=8．
11．已知a，b表示两条不同直线，α，β，γ表示三个不同平面，给出下列命题：
①若α∩β=a，b?α，a⊥b，则α⊥β；
②若a?α，a垂直于β内的任意一条直线，则α⊥β；
③若α⊥β，α∩β=a，α∩γ=b，则a⊥b；
④若a不垂直于平面α，则a不可能垂直于平面α内的无数条直线；
⑤若a⊥α，a⊥β，则α∥β．
上述五个命题中，正确命题的序号是②⑤．
12．已知集合A={x∈Z|（x+2）（x-1）＜0}，B={-2，-1}，那么A∪B等于（　　）
A．{-1}B．{-2，-1}C．{-2，-1，0}D．{-2，-1，0，1}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网