题目内容
5.函数$f(x)={(6-x-{x^2})^{\frac{3}{2}}}$的单调递减区间为( )| A. | $[{-\frac{1}{2},2}]$ | B. | $[{-3,-\frac{1}{2}}]$ | C. | $[-\frac{1}{2},+∞)$ | D. | $(-∞,-\frac{1}{2}]$ |
分析 求出函数f(x)的导数,解关于导函数的不等式,求出函数的递减区间即可.
解答 解:f′(x)=$\frac{3}{2}$${(6-x{-x}^{2})}^{\frac{1}{2}}$(-2x-1),
由题意令f′(x)≤0,
由$\left\{\begin{array}{l}{6-x{-x}^{2}≥0}\\{-2x-1≤0}\end{array}\right.$,解得:-$\frac{1}{2}$≤x≤2,
故选:A.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
15.任取一个3位正整数n,则对数log2n是一个正整数的概率为( )
| A. | $\frac{1}{225}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{450}$ | D. | 以上全不对 |
20.解α的终边过点P(4,-3),则cosα的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | 4 | D. | -3 |
10.“x>1”是“$\frac{1}{x}<1$”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知x,y满足线性约束条件$\left\{\begin{array}{l}y-x≤3\\ x+y≤5\\ y≥λ\end{array}\right.$,若z=x+4y的最大值与最小值之差为5,则实数λ的值为( )
| A. | 3 | B. | $\frac{7}{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
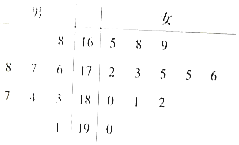 某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)