题目内容
6.已知数列{an},{bn}与函数f(x),{an}是首项a1=15,公差d≠0的等差数列,{bn}满足:bn=f(an).(1)若a4,a7,a8成等比数列,求d的值;
(2)若d=2,f(x)=|x-21|,求{bn}的前n项和Sn;
(3)若d=-1,f(x)=ex,Tn=b1•b2•b3…bn,问n为何值时,Tn的值最大?
分析 (1)由a4,a7,a8成等比数列,可得${a}_{7}^{2}$=a4•a8,可得(15+6d)2=(15+3d)(15+7d),化简解出即可得出..
(2)依题意,an=15+2(n-1)=2n+13,bn=|2n-8|,对n分类讨论,利用等差数列的求和公式即可得出.
(3)依题意,an=15-(n-1)=16-n,${b_n}={e^{16-n}}$,利用指数运算性质、等差数列的求和公式及其二次函数的单调性即可得出.
解答 解:(1)∵a4,a7,a8成等比数列,∴${a}_{7}^{2}$=a4•a8,∴(15+6d)2=(15+3d)(15+7d),化为:d2+2d=0,
∵d≠0,∴d=-2.
(2)依题意,an=15+2(n-1)=2n+13,bn=|2n-8|,
∴${b_n}=|2n-8|=\left\{\begin{array}{l}8-2n,n≤4\\ 2n-8,n>4\end{array}\right.$,
∴${S_n}=|{b_1}|+|{b_2}|+|{b_3}|+…+|{b_n}|=\left\{\begin{array}{l}7n-{n^2},n≤4\\{n^2}-7n+24,n>4\end{array}\right.$.
(3)依题意,an=15-(n-1)=16-n,${b_n}={e^{16-n}}$,
${T_n}={b_1}•{b_2}•{b_3}•…•{b_n}={e^{{a_1}+{a_2}+…+{a_n}}}={e^{-\frac{1}{2}({n^2}-31n)}}$,
∴当n=15或16时,Tn最大.
点评 本题考查了等差数列与等比数列的通项公式求和公式、二次函数的单调性、绝对值数列求和问题,考查了推理能力与就计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案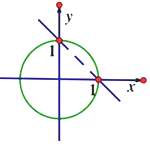
| A. | (x+y-1)•(x2+y2-1)=0 | B. | $\sqrt{x+y-1}•({x^2}+{y^2}-1)=0$ | ||
| C. | $(x+y-1)•\sqrt{{x^2}+{y^2}-1}=0$ | D. | $\sqrt{x+y-1}•\sqrt{{x^2}+{y^2}-1}=0$ |
| A. | 3 | B. | $\frac{7}{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
| A. | M=N | B. | M?N | C. | N?M | D. | M∩N=∅ |
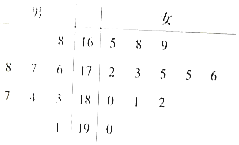 某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)