题目内容
8.定义在R上的奇函数f(x)满足f(x+1)=-$\frac{1}{f(x)}$.当x∈[0,1]时,f(x)=2x-1,则f($log_{\frac{1}{2}}{18}$)的值是-$\frac{1}{8}$.分析 由已知得f(x+2)=-$\frac{1}{f(x+1)}$=f(x),从而f($log_{\frac{1}{2}}{18}$)=f(-1-log29)=-f(1+log29)=-f(log29-3)=-$f(lo{g}_{2}\frac{9}{8})$,由此利用当x∈[0,1]时,f(x)=2x-1,能求出结果.
解答 解:∵在R上的奇函数f(x)满足f(x+1)=-$\frac{1}{f(x)}$.
∴f(x+2)=-$\frac{1}{f(x+1)}$=f(x),
∵当x∈[0,1]时,f(x)=2x-1,
∴f($log_{\frac{1}{2}}{18}$)=f(-1-log29)=-f(1+log29)=-f(log29-3)
=-$f(lo{g}_{2}\frac{9}{8})$=-(${2}^{lo{g}_{2}\frac{9}{8}}$-1)=-($\frac{9}{8}-1$)=-$\frac{1}{8}$.
故答案为:-$\frac{1}{8}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
18.某四棱锥的三视图如图所示,该四棱锥的表面积为( )


| A. | $1+\sqrt{2}$ | B. | 3 | C. | $2+\sqrt{2}$ | D. | 4 |
20.解α的终边过点P(4,-3),则cosα的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | 4 | D. | -3 |
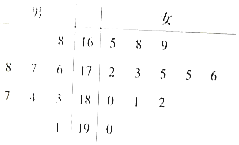 某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)