题目内容
S={1,2,…,2003},A是S的三元子集,满足:A中的所有元素可以组成等差数列.那么,这样的三元子集A的个数是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:等差数列的性质
专题:排列组合
分析:1,2,…,2003个数中有1002个奇数,1001个偶数,依题意,A中的三个数成等差数列,可分两类:①3个数中有至少2个奇数,②3个数中有至少2个偶数,利用组合数公式即可求得答案.
解答:
解:1,2,…,2003个数中有1002个奇数,1001个偶数,
依题意,A中的三个数成等差数列,可分两类:
①3个数中有至少2个奇数:从1002个奇数里边任意选两个,一定找到另外唯一的一个与这两个奇数构成等差数列,共有
种方法;
②3个数中有至少2个偶数:同理可得,共有
种方法;
综上所述,共有
+
个,
故选:B.
依题意,A中的三个数成等差数列,可分两类:
①3个数中有至少2个奇数:从1002个奇数里边任意选两个,一定找到另外唯一的一个与这两个奇数构成等差数列,共有
| C | 2 1002 |
②3个数中有至少2个偶数:同理可得,共有
| C | 2 1001 |
综上所述,共有
| C | 2 1001 |
| C | 2 1002 |
故选:B.
点评:本题考查等差数列的概念,突出考查排列组合的应用,考查等价转化思想与分类讨论思想的综合应用,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
规定:若函数f(x)的图象经过某种变换后所得图象对应函数的值域与f(x)的值域相同,则称这种变换是f(x)的T变换,下面给出四个函数及其对应的变换,其中不属于f(x)的T变换的是( )
| A、f(x)=(x-2)2:将函数f(x)的图象关于直线x=3对称 | ||||
| B、f(x)=2x-3-4:将函数f(x)的图象关于x轴对称 | ||||
| C、f(x)=2x-4:将函数f(x)的图象关于直线y=x对称 | ||||
D、f(x)=sin(2+
|
| C | 5 12 |
| C | 6 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列四个命题:
①时间、速度、加速度都是向量;
②零向量的长度为零,方向是任意的;
③若
,
是单位向量,则
=
;
④若非零向量
与
是共线向量,则A、B、C、D四点共线,其中正确命题的个数为( )
①时间、速度、加速度都是向量;
②零向量的长度为零,方向是任意的;
③若
| a |
| b |
| a |
| b |
④若非零向量
| AB |
| CD |
| A、0 | B、1 | C、2 | D、3 |
函数y=f(x)的图象与y轴的交点个数是( )
| A、至多一个 |
| B、至少一个 |
| C、必有一个 |
| D、一个、两个或无烽个 |
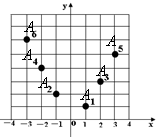 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1,A2,A3,A4,A5,A6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示,按如此规律下去,则a2011+a2012+a2013=
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1,A2,A3,A4,A5,A6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示,按如此规律下去,则a2011+a2012+a2013=