题目内容

矩阵M满足
12
21
M=
10
56
，设矩阵A=M5，求向量α=
5
1
经过矩阵A变换后得到的向量β．
考点：几种特殊的矩阵变换
专题：选作题,矩阵和变换
分析：先计算M=
34
-1-2
，再计算A=M5，即可求向量α=
5
1
经过矩阵A变换后得到的向量β．
解答： 解：∵
12
21
M=
10
56
，
∴M=
34
-1-2
，∴M2=
34
-1-2
2=
54
-10
，
∴A=M5=
34
-1-2
5=
8344
-19-12
，
∴
β
=
8344
-19-12
5
1
=
459
-107
点评：本题考查矩阵变换，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知函数g（x）满足g（x）=x-
4
x
，
（1）判断函数g（x）的奇偶性；
（2）求g（x）在区间[1，8]上的值域．
已知△ABC的三内角A、B、C满足条件
sin2A-(sinB-sinC)2
sinBsinC
=1，则角A等于
 
．
计算log36-log32+4 
1
2
-3 log34的结果为
 
．
集合M={-2，0，1，2}，N={x||2x-1|＞1}，则M∩N=（　　）
A、{-2，1，2}
B、{0，2}
C、{-2，2}
D、[-2，2]
已知函数f（x）
1-x
ax
+lnx，（a≠0）
（1）若函数f（x）在[1，+∞）上为增函数，求a的取值范围；
（2）当a=1时，求f（x）在区间(
1
2
，2)上的值域；
（3）当a=1时，问：是否存在正整数M，使得当自然数n≥M时，恒有lnn＞
1
2
+
1
3
+
1
4
+…+
1
n
成立？若存在，求出M的最小值，并证明你的结论；若不存在，说明理由．
已知直线l的极坐标方程是ρcosθ+ρsinθ-m=0．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，又知曲线C的参数方程是
x=2cosθ
y=sinθ
（θ为参数，θ∈[0，
2π
3
]），如果直线l与曲线C有且仅有一个公共点，求实数m的取值范围．
已知函数f（x）满足：①?s，t∈R有f（s+t）=f（s）+f（t）+st；②f（3）=6；③?x＞0，有f（x）＞0．
（1）求f（1）的值；
（2）证明；函数f（x）在（0，+∞）上单调递增；
（3）求满足f（2x）+f（2x+1）＜4的x的取值范围．
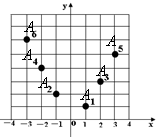如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：A1，A2，A3，A4，A5，A6的横纵坐标分别对应数列{an}（n∈N*）的前12项，如表所示，按如此规律下去，则a2011+a2012+a2013=
 
．
a1a2a3a4a5a6a7a8a9a10a11a12
x1y1x2y2x3y3x4y4x5y5x6y6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网