题目内容
已知g(x)=-loga
是奇函数(其中a>1)
(1)求m的值.
(2)判断g(x)在(1,+∞)上的单调性,并简要说明理由.
(3)当x∈(r,a-1)时,若g(x)的取值范围恰为(1,+∞),求a与r的值.
| 1-x |
| mx-1 |
(1)求m的值.
(2)判断g(x)在(1,+∞)上的单调性,并简要说明理由.
(3)当x∈(r,a-1)时,若g(x)的取值范围恰为(1,+∞),求a与r的值.
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)由函数g(x)是奇函数,可得出g(-x)=-g(x),由此方程恒成立,可得出参数m的方程,解出参数的值,再由对数的真数大于0得出x的不等式,解出函数的定义域即可;
(2)由于本题中参数a的取值范围未定,故应对它的取值范围分类讨论,判断函数的单调性再进行证明;
(3)由题设x∈(r,a-2)时,g(x)的值的范围恰为(1,+∞),可根据函数的单调性确定出两个参数a及r的方程,解方程得出两个参数的值.
(2)由于本题中参数a的取值范围未定,故应对它的取值范围分类讨论,判断函数的单调性再进行证明;
(3)由题设x∈(r,a-2)时,g(x)的值的范围恰为(1,+∞),可根据函数的单调性确定出两个参数a及r的方程,解方程得出两个参数的值.
解答:
解:(1)因为g(x)=-loga
=loga
是奇函数;
即1-m2x2=1-x2对定义域内的一切x都成立,
所以m2=1,m=±1,
由于
>0,所以m=-1;
所以g(x)=loga
,定义域为(-∞,-1)∪(1,+∞);
(2)当a>1时,g(x)=loga
,任取x1,x2∈(1,+∞),x1<x2,
则g(x1)-g(x2)=loga
-loga
=loga(
+1)-loga(
+1)
由于x1,x2∈(1,+∞),x1<x2,所以
+1>
+1,得g(x1)>g(x2),
所以g(x)在(1,+∞)上单调递减;
同理可得,当0<a<1时,g(x)在(1,+∞)上单调递增;
(3)因为x∈(r,a-2),定义域为(-∞,-1)∪(1,+∞),
1°当r≥1时,则1≤r<a-1,即a>2,
所以g(x)在(r,a-1)上为减函数,值域恰为(1,+∞),所以g(a-2)=1,
即loga
=loga
=1,即
=a,
所以a=2+
且r=1,
2°当r<1时,则(r,a-1)?(-∞,-1),所以0<a<1
因为g(x)在(r,a-1)上为增函数,
所以g(r)=1=a,与0<a<1矛盾.
所以a=2+
且r=1.
| 1-x |
| mx-1 |
| 1-mx |
| 1-x |
即1-m2x2=1-x2对定义域内的一切x都成立,
所以m2=1,m=±1,
由于
| 1-mx |
| 1-x |
所以g(x)=loga
| 1+x |
| x-1 |
(2)当a>1时,g(x)=loga
| 1+x |
| x-1 |
则g(x1)-g(x2)=loga
| 1+x1 |
| x1-1 |
| 1+x2 |
| x2-1 |
| 2 |
| x1-1 |
| 2 |
| x2-1 |
由于x1,x2∈(1,+∞),x1<x2,所以
| 2 |
| x1-1 |
| 2 |
| x2-1 |
所以g(x)在(1,+∞)上单调递减;
同理可得,当0<a<1时,g(x)在(1,+∞)上单调递增;
(3)因为x∈(r,a-2),定义域为(-∞,-1)∪(1,+∞),
1°当r≥1时,则1≤r<a-1,即a>2,
所以g(x)在(r,a-1)上为减函数,值域恰为(1,+∞),所以g(a-2)=1,
即loga
| 1+a-2 |
| a-2-1 |
| a-1 |
| a-3 |
| a-1 |
| a-3 |
所以a=2+
| 3 |
2°当r<1时,则(r,a-1)?(-∞,-1),所以0<a<1
因为g(x)在(r,a-1)上为增函数,
所以g(r)=1=a,与0<a<1矛盾.
所以a=2+
| 3 |
点评:本题考查了函数的单调性和奇偶性的运用以及对数的运算,属于中档题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
集合M={-2,0,1,2},N={x||2x-1|>1},则M∩N=( )
| A、{-2,1,2} |
| B、{0,2} |
| C、{-2,2} |
| D、[-2,2] |
y=kx+k,y=
在同一坐标系中的图象大致是( )
| k |
| x |
A、 |
B、 |
C、 |
D、 |
表示如图中阴影部分所示平面区域的不等式组是( )
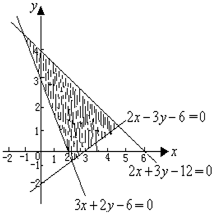

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
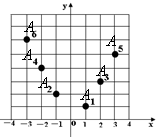 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1,A2,A3,A4,A5,A6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示,按如此规律下去,则a2011+a2012+a2013=
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1,A2,A3,A4,A5,A6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示,按如此规律下去,则a2011+a2012+a2013=