题目内容
已知函数f(x)=
,且f(2)=f(0),f(3)=9,则关于x的方程f(x)=x的解的个数为( )
|
| A、1 | B、2 | C、3 | D、4 |
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:由题意
从而解出b、c;从而解出方程的解.
|
解答:
解:由题意得,
解得,b=-4,c=3,
若x≥0,则方程f(x)=x可化为:
2x2-4x+3=x,
△=25-4×2×3=1>0,且-
=
,
=
;
故有两个正根,成立;
若x<0,则方程f(x)=x可化为:
x=-3,成立;
故选C.
|
解得,b=-4,c=3,
若x≥0,则方程f(x)=x可化为:
2x2-4x+3=x,
△=25-4×2×3=1>0,且-
| b |
| a |
| 5 |
| 2 |
| c |
| a |
| 3 |
| 2 |
故有两个正根,成立;
若x<0,则方程f(x)=x可化为:
x=-3,成立;
故选C.
点评:本题考查了函数的参数的求法,从而求出方程的解,从而求方程的解的个数.属于基础题.

练习册系列答案
相关题目
在极坐标系中,已知点A(2,
),B(2,π),点M是圆ρ=2cosθ上任意一点,则点M到直线AB的距离的最小值为( )
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=
的最大值是( )
| 2 |
| 1-x(1-x) |
A、
| ||
B、
| ||
C、
| ||
D、
|
| C | 5 12 |
| C | 6 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
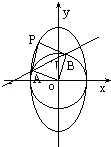 过椭圆C:
过椭圆C: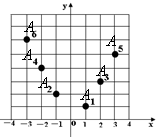 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1,A2,A3,A4,A5,A6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示,按如此规律下去,则a2011+a2012+a2013=
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1,A2,A3,A4,A5,A6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示,按如此规律下去,则a2011+a2012+a2013=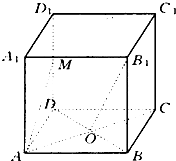 在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.
在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.