题目内容
20.过双曲线$\frac{{x}^{2}}{3}$-y2=1的两焦点作实轴的垂线,分别与渐近线交于A、B、C、D四点,则矩形ABCD的面积为( )| A. | $\frac{16}{3}$$\sqrt{3}$ | B. | 3 | C. | 8 | D. | 2 |
分析 求出双曲线的a,b,c,可得焦点坐标和渐近线方程,令x=2,x=-2求得矩形的顶点坐标,求出矩形ABCD的相邻两边长,即可得到所求面积.
解答 解:双曲线$\frac{{x}^{2}}{3}$-y2=1的a=$\sqrt{3}$,b=1,c=2,
则双曲线的焦点F1(-2,0),F2(2,0),
渐近线方程为y=±$\frac{\sqrt{3}}{3}$x,
令x=-2,可得y=±$\frac{2\sqrt{3}}{3}$;令x=2,可得y=±$\frac{2\sqrt{3}}{3}$.
则有A(-2,$\frac{2\sqrt{3}}{3}$),B(-2,-$\frac{2\sqrt{3}}{3}$),C(2,-$\frac{2\sqrt{3}}{3}$),D(2,$\frac{2\sqrt{3}}{3}$),
则矩形ABCD的面积为|AB|•|BC|=$\frac{4\sqrt{3}}{3}$×4=$\frac{16\sqrt{3}}{3}$.
故选:A.
点评 本题考查双曲线的方程和性质,考查渐近线方程的运用,求出矩形的顶点坐标是解题的关键.

练习册系列答案
相关题目
10.已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象上相邻两个最高点的距离为π.若将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度后,所得图象关于y轴对称.则函数f(x)的解析式为( )
| A. | f(x)=2sin(x+$\frac{π}{6}$) | B. | f(x)=2sin(x+$\frac{π}{3}$) | C. | f(x)=2sin(2x+$\frac{π}{6}$) | D. | f(x)=2sin(2x+$\frac{π}{3}$) |
15.已知双曲线的焦距为2$\sqrt{3}$,焦点到一条渐近线的距离为$\sqrt{2}$,则双曲线的标准方程为( )
| A. | x2-$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | ||
| C. | x2-$\frac{{y}^{2}}{2}$=1或y2-$\frac{{x}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-y2=1或$\frac{{y}^{2}}{2}$-x2=1 |
10.已知点P是抛物线y2=2x上的一个动点,则点P到点D$(2,\frac{3}{2}\sqrt{3})$的距离与点P到y轴的距离之和的最小值为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
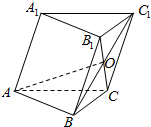 已知斜三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,∠BAA1=$\frac{2π}{3}$,∠CAA1=$\frac{π}{3}$,AB=AC=1,AA1=2,点O是B1C与BC1的交点.
已知斜三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,∠BAA1=$\frac{2π}{3}$,∠CAA1=$\frac{π}{3}$,AB=AC=1,AA1=2,点O是B1C与BC1的交点.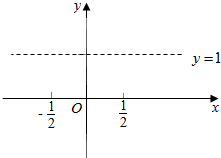 已知直线y=1与曲线y=x2-|x|+a有四个交点.
已知直线y=1与曲线y=x2-|x|+a有四个交点.