题目内容
18．已知$\overrightarrow{a}$=（sinα，cosα），$\overrightarrow{b}$=（$\sqrt{3}$，1），且$\overrightarrow{a}⊥\overrightarrow{b}$，那么sin（α+$\frac{π}{3}$）=（ ）| A． | -$\frac{1}{2}$或$\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
分析 $\overrightarrow{a}⊥\overrightarrow{b}$，可得$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{3}$sinα+cosα=0，化为tanα=-$\frac{\sqrt{3}}{3}$，解出即可得出．
解答 解：∵$\overrightarrow{a}⊥\overrightarrow{b}$，∴$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{3}$sinα+cosα=0，
∴tanα=-$\frac{\sqrt{3}}{3}$，可得α=kπ+$\frac{5π}{6}$或α=kπ+$\frac{11π}{6}$．（k∈Z）．
那么sin（α+$\frac{π}{3}$）=$±\frac{1}{2}$．
故选：A．
点评 本题考查了数量积运算性质、三角函数求值，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
6．设集合M={x|x2-2x＞0}，集合N={0，1，2，3，4}，则M∩N等于（ ）
| A． | {4} | B． | {3，4} | C． | {0，1，2} | D． | {0，1，2，3，4} |
13．
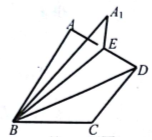如图，在直二面角A-BD-C中，△ABD、△CBD均是以BD为斜边的等腰直角三角形，取AD中点E，将△ABE沿BE翻折到△A1BE，在△ABE的翻折过程中，下列不可能成立的是（ ）
如图，在直二面角A-BD-C中，△ABD、△CBD均是以BD为斜边的等腰直角三角形，取AD中点E，将△ABE沿BE翻折到△A1BE，在△ABE的翻折过程中，下列不可能成立的是（ ）| A． | BC与平面A1BE内某直线平行 | B． | CD∥平面A1BE | ||
| C． | BC与平面A1BE内某直线垂直 | D． | BC⊥A1B |
3．已知sin（α+$\frac{π}{3}$）=$\frac{3}{5}$，则cos（$\frac{π}{6}$-α）的值是（ ）
| A． | -$\frac{3}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | -$\frac{4}{5}$ |