题目内容
3.已知sin(α+$\frac{π}{3}$)=$\frac{3}{5}$,则cos($\frac{π}{6}$-α)的值是( )| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
分析 由已知结合三角函数的诱导公式求得cos($\frac{π}{6}$-α)的值.
解答 解:∵sin(α+$\frac{π}{3}$)=$\frac{3}{5}$,
∴cos($\frac{π}{6}$-α)=sin[$\frac{π}{2}$-($\frac{π}{6}-α$)]=sin($α+\frac{π}{3}$)=$\frac{3}{5}$.
故选:B.
点评 本题考查三角函数的化简求值,考查了诱导公式的应用,是基础的计算题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.已知(x+$\frac{a}{x}$)n(n∈N,n>5)展开式的第5项是70,则展开式各项系数和是( )
| A. | 1 | B. | -1 | C. | 28或0 | D. | 29或0 |
18.已知$\overrightarrow{a}$=(sinα,cosα),$\overrightarrow{b}$=($\sqrt{3}$,1),且$\overrightarrow{a}⊥\overrightarrow{b}$,那么sin(α+$\frac{π}{3}$)=( )
| A. | -$\frac{1}{2}$或$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
8.已知△ABC的三个顶点A,B,C及△ABC所在平面内一点G,若$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow 0$,且实数λ满足$\overrightarrow{AB}+\overrightarrow{AC}=λ\overrightarrow{AG}$,则λ=( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | -1 | D. | 2 |
13.已知α,β为平面,a,b,c为直线,下列命题正确的是( )
| A. | 若a⊆α,b∥a,则b∥α | B. | 若α⊥β,α∩β=c,b⊥c,则b⊥β | ||
| C. | 若a⊥b,b⊥c,则a∥c | D. | 若a∩b=A,a⊆α,b⊆α,a∥β,b∥β,则α∥β |
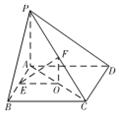 如图,四棱锥中P-ABCD,PA⊥平面ABCD,∠PDA=30°,O,E,F分别是AC,AB,PC的中点.
如图,四棱锥中P-ABCD,PA⊥平面ABCD,∠PDA=30°,O,E,F分别是AC,AB,PC的中点.