题目内容
13．
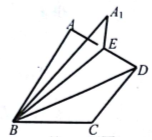如图，在直二面角A-BD-C中，△ABD、△CBD均是以BD为斜边的等腰直角三角形，取AD中点E，将△ABE沿BE翻折到△A1BE，在△ABE的翻折过程中，下列不可能成立的是（ ）| A． | BC与平面A1BE内某直线平行 | B． | CD∥平面A1BE | ||
| C． | BC与平面A1BE内某直线垂直 | D． | BC⊥A1B |
分析 构造平面BCE，平面BFE，则可判断A，B，C，使用假设法判断D．
解答 
解：连结CE，当平面A1BE与平面BCE重合时，BC?平面A1BE，
∴平面A1BE内必存在与BC平行和垂直的直线，故A，C可能成立；
在平面BCD内过B作CD的平行线BF，使得BF=CD，
连结EF，则当平面A1BE与平面BEF重合时，BF?平面A1BE，
故平面A1BE内存在与BF平行的直线，即平面A1BE内存在与CD平行的直线，
∴CD∥平面A1BE，故C可能成立．
若BC⊥A1B，又A1B⊥A1E，则A1B为直线A1E和BC的公垂线，
∴A1B＜CE，
设A1B=1，则经计算可得CE=$\frac{\sqrt{3}}{2}$，
与A1B＜CE矛盾，故D不可能成立．
故选D．
点评 本题考查了空间线面位置关系的判断，属于中档题．
练习册系列答案
相关题目
8．$\overrightarrow a=（sinα，1）$，$\overrightarrow b=（-2，4cosα）$，若$\overrightarrow a$与$\overrightarrow b$共线，则tanα=（ ）
| A． | 1 | B． | -1 | C． | ±1 | D． | $\sqrt{2}$ |
18．已知$\overrightarrow{a}$=（sinα，cosα），$\overrightarrow{b}$=（$\sqrt{3}$，1），且$\overrightarrow{a}⊥\overrightarrow{b}$，那么sin（α+$\frac{π}{3}$）=（ ）
| A． | -$\frac{1}{2}$或$\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
5．已知0＜α＜$\frac{π}{2}$＜β＜π，又sinα=$\frac{3}{5}$，cos（α+β）=-$\frac{4}{5}$，则sinβ=（ ）
| A． | 0 | B． | $\frac{24}{25}$ | C． | $\frac{16}{25}$ | D． | $\frac{24}{25}$或$\frac{16}{25}$ |