题目内容
7.已知直线l经过点M(1,6),且倾斜角为$\frac{π}{3}$,圆C的方程是x2+y2-2x-24=0,直线l与圆C交于P1,P2两点.(1)求圆心C到直线l的距离;
(2)求P1,P2两点间的距离.
分析 (1)由已知直线的倾斜角求出斜率,写出直线方程的点斜式,化为一般式,再化圆的方程为标准方程,求出圆心坐标和半径,由点到直线的距离公式求得圆心C到直线l的距离;
(2)由(1)中求得的点到直线的距离及圆的半径,结合垂径定理求得P1,P2两点间的距离.
解答 解:(1)由题设知,直线l的斜率为tan$\frac{π}{3}$=$\sqrt{3}$,
则直线方程为:y-6=$\sqrt{3}$(x-1),即$\sqrt{3}x-y+6-\sqrt{3}=0$,
圆C的方程可化为:(x-1)2+y2=25,
故圆心C的坐标为(1,0),圆C的半径r=5,
∴点C到直线l的距离d=$\frac{|\sqrt{3}×1-0+6-\sqrt{3}|}{\sqrt{(\sqrt{3})^{2}+(-1)^{2}}}=3$;
(2)由垂径定理可得|P1P2|=$2\sqrt{{r}^{2}-{d}^{2}}=2\sqrt{25-9}=8$.
点评 本题考查直线与圆位置关系的应用,考查点到直线的距离公式,是基础的计算题.

练习册系列答案
相关题目
18.已知$\overrightarrow{a}$=(sinα,cosα),$\overrightarrow{b}$=($\sqrt{3}$,1),且$\overrightarrow{a}⊥\overrightarrow{b}$,那么sin(α+$\frac{π}{3}$)=( )
| A. | -$\frac{1}{2}$或$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
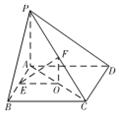 如图,四棱锥中P-ABCD,PA⊥平面ABCD,∠PDA=30°,O,E,F分别是AC,AB,PC的中点.
如图,四棱锥中P-ABCD,PA⊥平面ABCD,∠PDA=30°,O,E,F分别是AC,AB,PC的中点.