题目内容
过点(2,-4)且与曲线y=
相切的切线方程是 .
| 1 |
| x |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:设出切点坐标,利用导数的几何意义求出切线方程,利用过点(2,-4),求出切点坐标即可得到结论.
解答:
解:设切点A(x0,y0),
∵y′=-
,
∴切线斜率为k=-
,
∴对应的切线方程为y-
=-
(x-x0)=-
x+
,
即y=-
x+
,
又切线过(2,-4),
∴-4=-
+
,
即2x02+x0-1=0,
解得x0=-1或x0=
,
∴切线方程为:y=-x-2或y=-4x+4.
故答案为:y=-x-2或y=-4x+4
∵y′=-
| 1 |
| x2 |
∴切线斜率为k=-
| 1 |
| x02 |
∴对应的切线方程为y-
| 1 |
| x0 |
| 1 |
| x02 |
| 1 |
| x02 |
| 1 |
| x0 |
即y=-
| 1 |
| x02 |
| 2 |
| x0 |
又切线过(2,-4),
∴-4=-
| 2 |
| x02 |
| 2 |
| x0 |
即2x02+x0-1=0,
解得x0=-1或x0=
| 1 |
| 2 |
∴切线方程为:y=-x-2或y=-4x+4.
故答案为:y=-x-2或y=-4x+4
点评:考查学生会利用导数求切线上过某点切线方程的斜率,会根据斜率和一点坐标写出直线的方程,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
与命题“若p则q”的否命题真假相同的命题是( )
| A、若q 则p |
| B、若¬p则q |
| C、若¬q则p |
| D、若¬p则¬q |
若x,y满足不等式组
,且y+
x的最大值为2,则实数m的值为( )
|
| 1 |
| 2 |
| A、-2 | ||
B、-
| ||
| C、1 | ||
D、
|
如图在棱长均为2的正四棱锥P-ABCD中,点E为PC中点,则下列命题正确的是( )


A、BE平行面PAD,且直线BE到面PAD距离为
| ||||
B、BE平行面PAD,且直线BE到面PAD距离为
| ||||
C、BE不平行面PAD,且BE与平面PAD所成角大于
| ||||
D、BE不平行面PAD,且BE与面PAD所成角小于
|
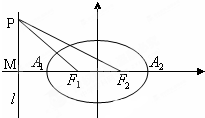 如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,A1,A2为左右顶点,焦距为2,左准线l与x轴的交点为M,|MA2|:|A1F1|=6:1.若点P在直线l上运动,且离心率e<
如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,A1,A2为左右顶点,焦距为2,左准线l与x轴的交点为M,|MA2|:|A1F1|=6:1.若点P在直线l上运动,且离心率e<