Question

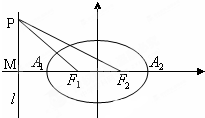如图，已知椭圆的中心在坐标原点，焦点F₁、F₂在x轴上，A₁，A₂为左右顶点，焦距为2，左准线l与x轴的交点为M，|MA₂|：|A₁F₁|=6：1．若点P在直线l上运动，且离心率e＜

1

2

，则tan∠F₁PF₂的最大值为

 

．

Answer 1

考点：椭圆的简单性质

专题：计算题,三角函数的求值,圆锥曲线的定义、性质与方程

分析：由椭圆的性质可得c=1，运用准线方程和离心率公式和两点距离公式，结合条件，可得a=2，再设P（-9，y），（y＞0），运用两角差的正切公式，结合基本不等式即可求得最大值．

解答： 解：由焦距为2，则c=1，
左准线l与x轴的交点为M，|MA₂|：|A₁F₁|=6：1，
则6（a-c）=a+

a2

c

，代入c=1，解得，a=2或3，
由于离心率e＜

1

2

，则a＞2c=2，则a=3．
则l：x=-9，
设P（-9，y），（y＞0），则MF₁|=8，|MF₂|=10，
则tan∠F₁PF₂=tan（∠F₂PM-∠F₁PM）=

10 y - 8 y

1+ 80 y2

=

2 y

1+ 80 y2

=

2

y+ 80 y

≤

2

2 y• 80 y

=

5

20

．
当且仅当y=

80

y

即y=4

5

时，取得最大值

5

20

．
故答案为：

5

20

．

点评：本题考查椭圆的性质：离心率和准线方程，考查三角函数的正切公式，考查基本不等式的运用：求最值，考查运算能力，属于中档题和易错题．