题目内容
△ABC中，已知a=
，b=1，C=30°，则△ABC的面积为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：正弦定理
专题：解三角形
分析：直接利用三角形的面积公式求解即可．
解答：
解：∵△ABC中，已知a=
，b=1，C=30°，
∴△ABC的面积S=
absinC=
×
×1×
=
．
故选：D．
| 3 |
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
故选：D．
点评：本题考查三角形的面积的求法，基本知识的考查．
练习册系列答案
考前必练系列答案
相关题目
设集合A={x|（x+3）（x-2）≤0}，B={x|y=
}，则A∩B（ ）
| 1 | ||
|
| A、（1，2） |
| B、[1，2] |
| C、[1，2） |
| D、（1，2] |
已知角θ的顶点与原点重合，始边与x轴的正半轴重合，终边在直线y=
x上，则sin2θ=（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是一个程序框图，则输出S的值是（ ）
| A、300 | B、330 |
| C、100 | D、150 |
已知函数y=sinax+b（a＞0）某一个周期的图象如图所示，则函数f（x）=ax2+bx+1零点的个数有（ ）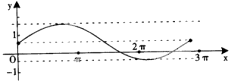
| A、0 | B、1 | C、2 | D、无法确定 |
已知集合U={0，1，2，3，4}，A={x|x2-2x=0}，则∁UA=（ ）
| A、{1，2，3} |
| B、{0，1，3，4} |
| C、{1，3，4} |
| D、{0，3，4} |
若实数x，y满足
，则z=x+2y的最小值是（ ）
|
| A、0 | ||
B、
| ||
| C、5 | ||
| D、1 |
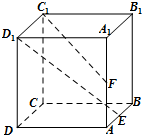已知点E、F分别是正方体ABCD-A1B1C1D1的棱AB、AA1的中点，点M、N分别是线段D1E与C1F上的点，则满足与平面ABCD平行的直线MN有（ ）