题目内容
已知函数y=sinax+b(a>0)某一个周期的图象如图所示,则函数f(x)=ax2+bx+1零点的个数有( )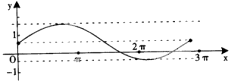

| A、0 | B、1 | C、2 | D、无法确定 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由函数函数y=sinax+b(a>0)在某一个周期的图象求得a与b的范围,得到二次函数的判别式小于0,从而得到二次函数的零点个数.
解答:
解:由函数y=sinax+b(a>0)的图象可得 0<b<1,2π<
<3π,即
<a<1.
由△=b2-4ac=b2-4a,
∵0<b<1,
<a<1,
∴b2-4a<0.
即函数f(x)=ax2+bx+1的图象与x轴没有交点.
∴函数f(x)=ax2+bx+1零点的个数为0.
故选:A.
| 2π |
| a |
| 2 |
| 3 |
由△=b2-4ac=b2-4a,
∵0<b<1,
| 2 |
| 3 |
∴b2-4a<0.
即函数f(x)=ax2+bx+1的图象与x轴没有交点.
∴函数f(x)=ax2+bx+1零点的个数为0.
故选:A.
点评:本题考查y=Asin(ωx+φ)型函数的图象与解析式,考查了二次函数的零点判断方法,是中低档题.

练习册系列答案
相关题目
若复数z满足(1+i)•z=i,则z的虚部为( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
若(x-
)n展开式的二项式系数之和为64,则展开式的常数项为( )
| 1 |
| x |
| A、10 | B、-20 |
| C、20 | D、-120 |
△ABC中,已知a=
,b=1,C=30°,则△ABC的面积为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点F(
,0),A(-1,0),B(1,0),直线x=
上有两个动点M,N,始终使∠MFN=45°,三角形MFN的外心轨迹为曲线C,P为曲线C在一象限内的动点,设∠PAB=α,∠PBA=β,∠APB=γ,则( )
| 2 |
| ||
| 2 |
| A、tanα+tanβ+tanγ=0 |
| B、tanα+tanβ-tanγ=0 |
| C、tanα+tanβ+2tanγ=0 |
| D、tanα+tanβ-2tanγ=0 |
将一枚质地均匀的骰子抛掷一次出现“正面向上的点数为2或3”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A={x||x+1|>0},B={-2,-1,0,1},则(∁RA)∩B=( )
| A、{-1} |
| B、{-2,0,1} |
| C、{0,1} |
| D、{-2} |
抛物线y2=16x的焦点坐标是( )
| A、(4,0) |
| B、(0,4) |
| C、(8,0) |
| D、(0,8) |