题目内容
5.已知椭圆M的对称轴为坐标轴,抛物线y2=4x的焦点F是椭圆M的一个焦点,且椭圆M的离心率为$\frac{\sqrt{2}}{2}$.(1)求椭圆M的方程;
(2)已知直线y=x+m与椭圆M交于A,B两点,且椭圆M上存在点P,满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,求m的值.
分析 (1)由已知椭圆M的一个焦点F(1,0),e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$,由此能求出椭圆M的方程.
(2)联立$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得3x2+4mx+2m2-2=0,由此利用韦达定理、向量、椭圆性质能求出m的值.
解答 解:(1)∵椭圆M的对称轴为坐标轴,抛物线y2=4x的焦点F是椭圆M的一个焦点,且椭圆M的离心率为$\frac{\sqrt{2}}{2}$,
∴椭圆M的一个焦点F(1,0),
设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
∵e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$,∴b=c=1,a=$\sqrt{2}$,
∴椭圆M的方程为:$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(2)设A(x1,y1),B(x2,y2),联立$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得3x2+4mx+2m2-2=0,
△=(4m)2-12(2m2-2)=-8m2+24>0,
解得-$\sqrt{3}<m<\sqrt{3}$,
∵$\overrightarrow{OP}$=$\overrightarrow{OA}+\overrightarrow{OB}$,∴P(x1+x2,y1+y2),
∵${x}_{1}+{x}_{2}=-\frac{4}{3}m$,${y}_{1}+{y}_{2}=\frac{2}{3}m$,
∴P(-$\frac{4}{3}m,\frac{2}{3}m$)在椭圆$\frac{{x}^{2}}{2}+{y}^{2}$=1上,
∴(-$\frac{4}{3}m$)2+2($\frac{2}{3}m$)2=2,
解得m=$±\frac{\sqrt{3}}{2}$.
点评 本题考查椭圆方程的求法,考查满足条件的实数值的求法,是中档题,解题时要认真审题,注意椭圆性质、向量知识、直线方程、抛物线等知识点的合理运用.

| A. | 1≤a≤2 | B. | a<1或a≥2 | C. | 1<a≤2 | D. | a<1或a>2 |
| A. | 20km | B. | 20$\sqrt{3}$km | C. | 20$\sqrt{5}$km | D. | 20$\sqrt{7}$km |
| A. | -$\frac{11}{4}$ | B. | 1 | C. | $\frac{19}{4}$ | D. | $\frac{21}{4}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
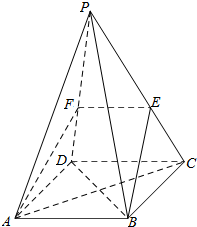 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PB=PD,过AB的平面分别交棱PC,PD于点E,F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PB=PD,过AB的平面分别交棱PC,PD于点E,F.