题目内容
10.袋中有大小相同4个小球,编号分别为1,2,3,4,从袋中任取两个球(不放回),则这两个球编号正好相差1的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 先求出基本事件总数,再由列举法这两个球编号正好相差1,由此能求出这两个球编号正好相差1的概率.
解答 解:一个袋子中有号码为1,2,3,4大小相同的4个小球,
从袋中任取两个球(不放回),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)基本事件总数为6个,
这两个球编号正好相差1基本事件有:(1,2),(2,3),(3,4),共3个,
∴则这两个球编号正好相差1的概率是$\frac{3}{6}$=$\frac{1}{2}$,
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知函数f(x)=$\left\{\begin{array}{l}{{4}^{x},x>0}\\{f(x+1)-1,x<0}\end{array}\right.$,则f(-$\frac{1}{2}$)+f($\frac{1}{2}$)=( )
| A. | 3 | B. | 5 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
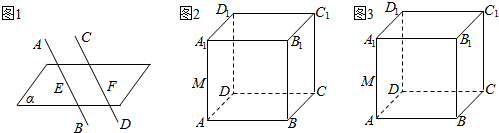
 如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD是菱形.过AB的平面与侧棱CC1,DD1分别交于点E,F.
如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD是菱形.过AB的平面与侧棱CC1,DD1分别交于点E,F.