Question

直线x=t、y=x将圆x²+y²=4分成若干块，现用5种不同的颜色给这若干块涂色，且共边的颜色不同，每块只涂一色，共有260种涂法，则实数t的取值范围是

 

．

Answer 1

考点：排列、组合的实际应用

专题：应用题,排列组合

分析：由题意知x=t、y=x两直线的交点必在y=x这条直线上，而要想使任意两块不同色共有涂法260种，必须让直线x=m，y=x将圆分成四块不同的面积，要求出y=x与圆的交点，得到结果．

解答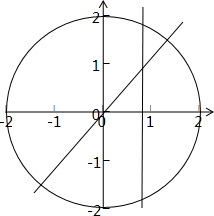： 解：由题意知x=t、y=x两直线的交点必在y=x这条直线上，
而要想使任意两块不同色共有涂法260种，
∵

C

4 5

A

4 4

+

C

3 5

C

1 3

×2×2+

C

2 5

×2=260，
∴直线把圆分成了4部分，即必须让直线x=t、y=x将圆分成四块不同的面积，
求出y=x与圆的交点分别为（-

2

，-

2

）（

2

，

2

）．
∴-

2

≤t≤

2

，
∵当t=

2

或-

2

时，两直线只能把该圆分成三个区域，
∴不成立，
∴-

2

＜t＜

2

，
故答案为：-

2

＜t＜

2

．

点评：本题考查排列组合问题在解析几何中的应用，在计算时要求做到，兼顾所有的条件，注意实际问题本身的限制条件．