题目内容
正方体的内切球的体积为36π，则此正方体的表面积是（V球体=
πR3（R为球的半径））（ ）
| 4 |
| 3 |
| A、216 | B、72 |
| C、108 | D、648 |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：正方体的内切球的直径与正方体的边长相等，即可得出结论．
解答：
解：∵正方体的内切球体积为36π，
∴内切球的半径为3，
∵正方体的内切球的直径与正方体的边长相等，
∴正方体的边长为6．
故该正方体的表面积为：62×6=216．
故选：A．
∴内切球的半径为3，
∵正方体的内切球的直径与正方体的边长相等，
∴正方体的边长为6．
故该正方体的表面积为：62×6=216．
故选：A．
点评：本题考查了学生的空间想象力，考查学生的计算能力，属于基础题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
与双曲线x2-
=1有共同渐近线，且过点（2，
）的双曲线方程是（ ）
| y2 |
| 2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列{an}的通项公式为an=（-1）n+1•
，则a7=（ ）
| n+1 |
| n |
| A、8 | ||
B、-
| ||
C、
| ||
| D、7 |
用反证法证明命题“若整系数一元二次方程ax2+bx+c=0（a≠0）有有理根，那么a，b，c中至少有一个是偶数”时，下列假设中正确的是（ ）
| A、假设a，b，c不都是偶数 |
| B、假设a，b，c都不是偶数 |
| C、假设a，b，c至多有一个是偶数 |
| D、假设a，b，c至多有两个是偶数 |
如图所示，在边长为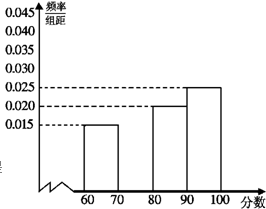
某集团公司对所属的200家企业进行年终考评，并依据考评得分（最低60分，最高100分，可以是小数）将其分别评定为A、B、C、D四个等级，标准如下表：