题目内容
已知直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R),圆C:(x-1)2+(y-2)2=25.
(Ⅰ)证明:直线l与圆C相交;
(Ⅱ)当直线l被圆C截得的弦长最短时,求m的值.
(Ⅰ)证明:直线l与圆C相交;
(Ⅱ)当直线l被圆C截得的弦长最短时,求m的值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(Ⅰ)通过直线l转化为直线系,求出直线恒过的定点,判断定点与圆的位置故选即可判断直线l与圆C相交;
(Ⅱ)说明直线l被圆C截得的弦长最小时,圆心与定点连线与直线l垂直,求出斜率即可求出直线的方程.
(Ⅱ)说明直线l被圆C截得的弦长最小时,圆心与定点连线与直线l垂直,求出斜率即可求出直线的方程.
解答:
解:(Ⅰ)直线l方程变形为(2x+y-7)m+(x+y-4)=0,
由
,得
,所以直线l恒过定点P(3,1),…(2分)
又|PC|=
<5,故P点在圆C内部,所以直线l与圆C相交;…(4分)
(Ⅱ)当l⊥PC时,所截得的弦长最短,此时有kl•kPC=-1,…(6分)
而kl=-
,kPC=-
,于是
=-1,解得m=-
.…(8分)
由
|
|
又|PC|=
| 5 |
(Ⅱ)当l⊥PC时,所截得的弦长最短,此时有kl•kPC=-1,…(6分)
而kl=-
| 2m+1 |
| m+1 |
| 1 |
| 2 |
| 2m+1 |
| 2(m+1) |
| 3 |
| 4 |
点评:本题考查直线系方程的应用,考查直线与圆的位置关系,考查转化思想,函数与方程的思想的应用,考查计算能力.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
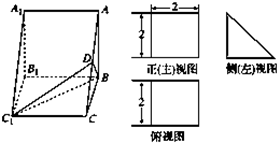 直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )
直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )| A、AB1∥平面BDC1 | ||
| B、A1C⊥平面BDC1 | ||
| C、直三棱柱的体积V=4 | ||
D、直三棱柱的外接球的表面积为4
|
圆柱的侧面展开图是一个边长为2和4的矩形,则圆柱的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |
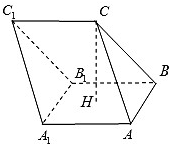 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.