题目内容
两条直线l1:
-
=1和l2:
-
=1在同一直角坐标系中的图象可以是( )
| x |
| a |
| y |
| b |
| x |
| b |
| y |
| a |
A、 |
B、 |
C、 |
D、 |
考点:直线的截距式方程
专题:直线与圆
分析:由方程得出直线的截距,逐个选项验证可得.
解答:
解:由截距式方程可得直线l1的横、纵截距分别为a,-b,
直线l2的横、纵截距分别为b,-a,
选项A,由l1的图象可得a<0,b>0,可得直线l2的截距均为正数,故正确;
选项B,只有当a=-b时,才有直线平行,故错误;
选项C,只有当a=b时,才有直线的纵截距相等,故错误;
选项D,由l1的图象可得a>0,b>0,可得直线l2的横截距为正数,纵截距为负数,
由图象不对应,故错误.
故选:A.
直线l2的横、纵截距分别为b,-a,
选项A,由l1的图象可得a<0,b>0,可得直线l2的截距均为正数,故正确;
选项B,只有当a=-b时,才有直线平行,故错误;
选项C,只有当a=b时,才有直线的纵截距相等,故错误;
选项D,由l1的图象可得a>0,b>0,可得直线l2的横截距为正数,纵截距为负数,
由图象不对应,故错误.
故选:A.
点评:本题考查直线的截距式方程,属基础题.

练习册系列答案
相关题目
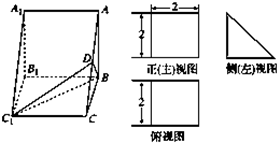 直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )
直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )| A、AB1∥平面BDC1 | ||
| B、A1C⊥平面BDC1 | ||
| C、直三棱柱的体积V=4 | ||
D、直三棱柱的外接球的表面积为4
|
已知a=sin15°cos15°,b=cos2
-sin2
,c=
,则a,b,c的大小关系是( )
| π |
| 6 |
| π |
| 6 |
| tan30° |
| 1-tan230° |
| A、a<b<c |
| B、a>b>c |
| C、c>a>b |
| D、a<c<b |
把1010(2)化为十进制数为( )
| A、20 | B、12 | C、10 | D、11 |
方程x2+y2-2x+4y+1=0所表示的图形的面积是( )
| A、π | ||
| B、2π | ||
| C、4π | ||
D、
|
 如图,直三棱柱ABC-A1B1C1中,点D是BC上一点.
如图,直三棱柱ABC-A1B1C1中,点D是BC上一点.