题目内容
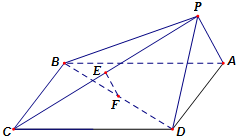 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.(Ⅰ)若E,F分别为PC,BD中点,求证:EF∥平面PAD;
(Ⅱ)求证:PA⊥CD;
(Ⅲ)若PA=PD=
| ||
| 2 |
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)连结AC.由正方形性质得AC与BD互相平分,由三角形中位线定理得EF∥PA.由此能证明EF∥平面PAD.
(Ⅱ)由线面垂直得CD⊥AD,所以CD⊥面PAD.由此能证明PA⊥CD.
(Ⅲ)由勾股定理得PA⊥PD.再由PA⊥CD,得PA⊥平面PCD.由此能证明面PAB⊥平面PCD.
(Ⅱ)由线面垂直得CD⊥AD,所以CD⊥面PAD.由此能证明PA⊥CD.
(Ⅲ)由勾股定理得PA⊥PD.再由PA⊥CD,得PA⊥平面PCD.由此能证明面PAB⊥平面PCD.
解答:
 (本小题满分14分)
(本小题满分14分)
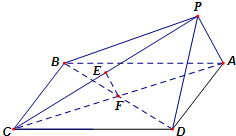
(Ⅰ)证明:如图,连结AC.因为底面ABCD是正方形,
所以AC与BD互相平分.
又因为F是BD中点,所以F是AC中点.
在△PAC中,E是PC中点,F是AC中点,
所以EF∥PA.
又因为EF?平面PAD,PA?平面PAD,
所以EF∥平面PAD.…(4分)
(Ⅱ)证明:因为平面PAD⊥底面ABCD,
且平面PAD∩平面ABCD=AD,
又CD⊥AD,所以CD⊥面PAD.
又因为PA?平面PAD,
所以CD⊥PA.故PA⊥CD.…(9分)
(Ⅲ)证明:在△PAD中,因为PA=PD=
AD,
所以PA⊥PD.
由(Ⅱ)可知PA⊥CD,且CD∩PD=D,
所以PA⊥平面PCD.
又因为PA?平面PAB,
所以面PAB⊥平面PCD.…(14分)
 (本小题满分14分)
(本小题满分14分)(Ⅰ)证明:如图,连结AC.因为底面ABCD是正方形,
所以AC与BD互相平分.
又因为F是BD中点,所以F是AC中点.
在△PAC中,E是PC中点,F是AC中点,
所以EF∥PA.
又因为EF?平面PAD,PA?平面PAD,
所以EF∥平面PAD.…(4分)
(Ⅱ)证明:因为平面PAD⊥底面ABCD,
且平面PAD∩平面ABCD=AD,
又CD⊥AD,所以CD⊥面PAD.
又因为PA?平面PAD,
所以CD⊥PA.故PA⊥CD.…(9分)
(Ⅲ)证明:在△PAD中,因为PA=PD=
| ||
| 2 |
所以PA⊥PD.
由(Ⅱ)可知PA⊥CD,且CD∩PD=D,
所以PA⊥平面PCD.
又因为PA?平面PAB,
所以面PAB⊥平面PCD.…(14分)
点评:本题考查直线与平面平行的证明,考查异面直线垂直的证明,考查平面与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)左、右焦点分别为F1(-c,0),F2(c,0),若双曲线右支上存在点P使得
=
,则该双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| sin∠PF1F2 |
| c |
| sin∠PF2F1 |
A、(0,
| ||
B、(
| ||
C、(1,
| ||
D、(
|
已知f(x)=x3-4,则零点一定在( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(5,6) |
若不等式|x+1|-|x-2|>a在R上有解,则实数a的取值范围是( )
| A、a<3 | B、a>3 |
| C、a<1 | D、a>1 |
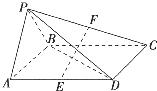 四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=
四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=