题目内容
已知双曲线
-
=1(a>0,b>0)左、右焦点分别为F1(-c,0),F2(c,0),若双曲线右支上存在点P使得
=
,则该双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| sin∠PF1F2 |
| c |
| sin∠PF2F1 |
A、(0,
| ||
B、(
| ||
C、(1,
| ||
D、(
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:△PF1F2中,由正弦定理得
=
,再由已知得
=
,根据P在双曲线右支上,得关于e的不等式,从而求出e的范围.
| |PF1| |
| sin∠PF2F1 |
| |PF2| |
| sin∠PF1F2 |
| |PF1| |
| |PF2| |
| c |
| a |
解答:
解:由题意,点P不是双曲线的顶点,否则
=
无意义;
在△PF1F2中,由正弦定理得
=
;
又
=
,∴
=
,
即|PF1|=
•|PF2|;
∵P在双曲线的右支上,由双曲线的定义,得
|PF1|-|PF2|=2a,
∴
•|PF2|-|PF2|=2a,即|PF2|=
;
由双曲线的几何性质,知
|PF2|>c-a,
∴
>c-a,
即c2-2ac-a2<0;
∴e2-2e-1<0,
解得-
+1<e<
+1;
又e>1,
∴双曲线离心率的范围是(1,
+1).
故选:C.
| a |
| sin∠PF1F2 |
| c |
| sin∠PF2F1 |
在△PF1F2中,由正弦定理得
| |PF1| |
| sin∠PF2F1 |
| |PF2| |
| sin∠PF1F2 |
又
| a |
| sin∠PF1F2 |
| c |
| sin∠PF2F1 |
| |PF1| |
| |PF2| |
| c |
| a |
即|PF1|=
| c |
| a |
∵P在双曲线的右支上,由双曲线的定义,得
|PF1|-|PF2|=2a,
∴
| c |
| a |
| 2a2 |
| c-a |
由双曲线的几何性质,知
|PF2|>c-a,
∴
| 2a2 |
| c-a |
即c2-2ac-a2<0;
∴e2-2e-1<0,
解得-
| 2 |
| 2 |
又e>1,
∴双曲线离心率的范围是(1,
| 2 |
故选:C.
点评:本题考查了求双曲线的离心率的范围的问题,也考查了双曲线的定义与简单性质的灵活运用问题,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
用柯西不等式求函数y=
+
+
的最大值为( )
| 2x-3 |
| 2x |
| 7-3x |
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
C
+2C
+C
等于( )
97 98 |
96 98 |
95 98 |
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
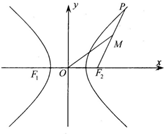 如图,双曲线
如图,双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线的离心率为2,焦点是(6,0),(-6,0),则双曲线的方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a1=12,a2=12+22+12,…,an=12+22+…+n2+…+22+12,在运用数学归纳法证明an=
n(2n2+1)时,第二步中从k到k+1应添加的项是( )
| 1 |
| 3 |
| A、k2+1 |
| B、(k2+1)2 |
| C、(k+1)2+k2 |
| D、(k+1)2+2k2 |
过△ABC所在平面α外一点P,作PO⊥α,垂足为O,连接PA,PB,PC.若PA=PB=PC,则点O是△ABC的( )
| A、垂心 | B、外心 | C、内心 | D、重心 |
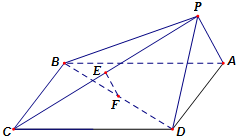 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.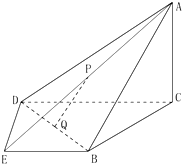 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=