题目内容
从1,2,3,4,5,6,8中任取两个不同的数,事件A为“取到的两个数的和为偶数”,事件B为“取到的两个数均为偶数“,则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:条件概率与独立事件
专题:概率与统计
分析:用列举法求出事件A为“取到的两个数的和为偶数”,事件B为“取到的两个数均为偶数”所包含的基本事件的个数,求p(A),P(AB),根据条件概率公式,即可得到结论.
解答:
解:从1,2,3,4,5,6,8中任取两个不同的数有
=21
事件A=“取到的两个数之和为偶数”所包含的基本事件有:(1,3)、(1,5)、(3,5)、(2,4),(2,6),(2,8),(4,6),(4,8),(6,8)共9个,
故P(A)=
=
,
事件B=“取到的两个数均为偶数”所包含的基本事件有(2,4),(2,6),(2,8),(4,6),(4,8),(6,8)共6个,
故P(AB)=
=
∴P(B|A)=
=
,
故选:B
| C | 2 7 |
事件A=“取到的两个数之和为偶数”所包含的基本事件有:(1,3)、(1,5)、(3,5)、(2,4),(2,6),(2,8),(4,6),(4,8),(6,8)共9个,
故P(A)=
| 9 |
| 21 |
| 3 |
| 7 |
事件B=“取到的两个数均为偶数”所包含的基本事件有(2,4),(2,6),(2,8),(4,6),(4,8),(6,8)共6个,
故P(AB)=
| 6 |
| 21 |
| 2 |
| 7 |
∴P(B|A)=
| P(AB) |
| P(A) |
| 2 |
| 3 |
故选:B
点评:本题考查条件概率的计算公式,同时考查学生对基础知识的记忆、理解和熟练程度.属于基础题

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
用柯西不等式求函数y=
+
+
的最大值为( )
| 2x-3 |
| 2x |
| 7-3x |
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
不等式(x+1)(x-2)<0的解集是( )
| A、(-∞,-2) |
| B、(-2,1) |
| C、(-∞,-1)∪(2,+∞) |
| D、(-1,2) |
在每学年学生的评优评先中,某班获得5个推荐名额,其中优秀干部1名,三好生2名,文明生2名,并且三好生和文明生都要求必须有男生参加,班级通过选举定下3男2女共5个推荐对象,则不同推荐方法的种数是( )
| A、36 | B、24 | C、22 | D、20 |
抛物线y2=8x的焦点与椭圆
+
=1的焦点重合,则椭圆的离心率为( )
| x 2 |
| a 2 |
| y 2 |
| 5 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
C
+2C
+C
等于( )
97 98 |
96 98 |
95 98 |
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
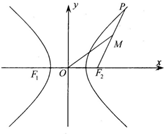 如图,双曲线
如图,双曲线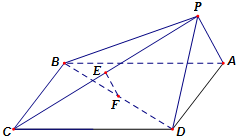 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.