题目内容
将函数y=sinπx在区间（0，+∞）内的全部零点按从小到大的顺序排成数列{an}．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）令bn=2nan，其中n∈N*，求数列{bn}的前n项和Tn．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）令bn=2nan，其中n∈N*，求数列{bn}的前n项和Tn．
考点：数列的求和,正弦函数的图象
专题：等差数列与等比数列
分析：（Ⅰ）求出函数的零点，得到数列{an}是等差数列，即可求数列{an}的通项公式；
（Ⅱ）求出bn=2nan，其中n∈N*的通项公式，利用错位相减法即可求数列{bn}的前n项和Tn．
（Ⅱ）求出bn=2nan，其中n∈N*的通项公式，利用错位相减法即可求数列{bn}的前n项和Tn．
解答：
解：（Ⅰ）由y=sinπx=0得，πx=nπ，即x=n，n∈N•，
它在（0，+∞）内的全部零点构成以1为首项，1为公差的等差数列，
则数列{an}的通项公式an=n．
（Ⅱ）∵bn=2nan=n•2n，
则数列{bn}的前n项和Tn=1•2+2•22+3•23+…+（n-1）•2n-1+n•2n，①
则2Tn=1•22+2•23+…+（n-1）•2n+n•2n+1，②
①-②得，-Tn=2+22+23+…+•2n-n•2n+1=
-n•2n+1=（1-n）•2n+1-2，
则Tn=2+（n-1）•2n+1．
它在（0，+∞）内的全部零点构成以1为首项，1为公差的等差数列，
则数列{an}的通项公式an=n．
（Ⅱ）∵bn=2nan=n•2n，
则数列{bn}的前n项和Tn=1•2+2•22+3•23+…+（n-1）•2n-1+n•2n，①
则2Tn=1•22+2•23+…+（n-1）•2n+n•2n+1，②
①-②得，-Tn=2+22+23+…+•2n-n•2n+1=
| 2(1-2n) |
| 1-2 |
则Tn=2+（n-1）•2n+1．
点评：本题主要考查等比数列的应用及数列求和，根据错位相减法是解决本题的关键．
练习册系列答案
相关题目
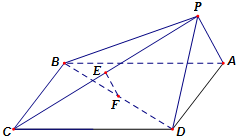如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD．
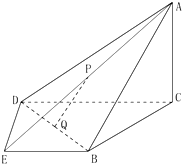如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC=
如图，已知几何体的底面ABCD为正方形，AC∩DB=N，PD⊥面ABCD，EC∥PD，PD=CD=2EC=2．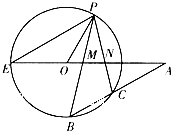
如图，E，P，B，C为圆O上的四点，直线PB，PC，BC分别交直线EO于M，N三点，且PM=PN．