题目内容
已知f（x）=x3-4，则零点一定在（ ）
| A、（1，2） |
| B、（2，3） |
| C、（3，4） |
| D、（5，6） |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：根据函数零点的判断条件，分别验证函数在端点处的符号，即可得到结论．
解答：
解：∵f（x）=x3-4，
∴f（1）=1-4=-3＜0，
f（2）=23-4=8-4=4＞0，
满足f（1）f（2）＜0，
即f（x）=x3-4的零点所在的区间为（1，2），
故选：A．
∴f（1）=1-4=-3＜0，
f（2）=23-4=8-4=4＞0，
满足f（1）f（2）＜0，
即f（x）=x3-4的零点所在的区间为（1，2），
故选：A．
点评：本题主要考查函数零点区间的判断，分别把端点值代入分别判断函数的符号时解决本题的关键．
练习册系列答案
相关题目
不等式（x+1）（x-2）＜0的解集是（ ）
| A、（-∞，-2） |
| B、（-2，1） |
| C、（-∞，-1）∪（2，+∞） |
| D、（-1，2） |
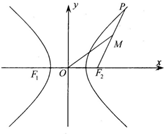如图，双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a1=12，a2=12+22+12，…，an=12+22+…+n2+…+22+12，在运用数学归纳法证明an=
n（2n2+1）时，第二步中从k到k+1应添加的项是（ ）
| 1 |
| 3 |
| A、k2+1 |
| B、（k2+1）2 |
| C、（k+1）2+k2 |
| D、（k+1）2+2k2 |
过△ABC所在平面α外一点P，作PO⊥α，垂足为O，连接PA，PB，PC．若PA=PB=PC，则点O是△ABC的（ ）
| A、垂心 | B、外心 | C、内心 | D、重心 |
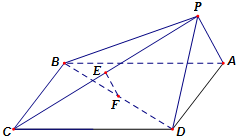如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD．