题目内容
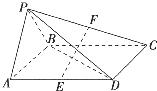 四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=
四棱锥P-ABCD的底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=| 1 |
| 2 |
(1)求证:EF⊥平面PBD;
(2)若AB=2,求四棱锥P-ABCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)取PB的中点G,连接FG,AG,不难证明四边形EFGA是平行四边形,则EF∥AG,又△PAB是等边三角形,有AG⊥PB①;另外,可以通过计算得到BD⊥AB,结合着平面PAB⊥平面ABCD,得到DB⊥平面PAB,从而DB⊥AG②.由①②知,AG⊥平面PBD,于是EF⊥平面PBD.
(2)由平面PAB⊥平面ABCD,知四棱锥P-ABCD的高为正三角形PAB的高,再分别计算代入体积公式即可.
(2)由平面PAB⊥平面ABCD,知四棱锥P-ABCD的高为正三角形PAB的高,再分别计算代入体积公式即可.
解答:
证明:(1)取PB的中点G,连接FG,AG,由题设,FG∥BC,FG=
BC,
∵AE∥BC,AE=
BC,∴EF∥AG.
△PAB是等边三角形,AG⊥PB,①
△ABD中,AD=2AB,∠BAD=60°,由余弦定理,
BD2=AB2+AD2-2AB×AD×cos60°=AD2-AB2.
∴∠BAD=90°.
∴BD⊥AB.
又因为平面PAB⊥平面ABCD,BD⊥AB,
∴DB⊥平面PAB,
∴DB⊥AG.②
由①②可知,AG⊥PB,AG⊥BD
∴AG⊥平面PBD.
∴EF⊥平面PBD.
(2)∵AB=2,∴PA=PB=
AD=2.
又ABCD是平行四边形,且∠BAD=60°,
故SABCD=2×4sin60°=4
,
又平面PAB⊥平面ABCD,
故四棱锥P-ABCD的高为正三角形PAB的高,即h=
.
∴四棱锥P-ABCD的体积为
×4
×
=4.
| 1 |
| 2 |
∵AE∥BC,AE=
| 1 |
| 2 |
△PAB是等边三角形,AG⊥PB,①
△ABD中,AD=2AB,∠BAD=60°,由余弦定理,
BD2=AB2+AD2-2AB×AD×cos60°=AD2-AB2.
∴∠BAD=90°.
∴BD⊥AB.
又因为平面PAB⊥平面ABCD,BD⊥AB,
∴DB⊥平面PAB,
∴DB⊥AG.②
由①②可知,AG⊥PB,AG⊥BD
∴AG⊥平面PBD.
∴EF⊥平面PBD.
(2)∵AB=2,∴PA=PB=
| 1 |
| 2 |
又ABCD是平行四边形,且∠BAD=60°,
故SABCD=2×4sin60°=4
| 3 |
又平面PAB⊥平面ABCD,
故四棱锥P-ABCD的高为正三角形PAB的高,即h=
| 3 |
∴四棱锥P-ABCD的体积为
| 1 |
| 3 |
| 3 |
| 3 |
点评:本题考查平面图形与空间图形的转化,考查线面垂直的判断,面面垂直的性质及空间几何体的体积计算等问题,考查学生的空间想象能力、推理能力和运算能力,难度适中.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
抛物线y2=8x的焦点与椭圆
+
=1的焦点重合,则椭圆的离心率为( )
| x 2 |
| a 2 |
| y 2 |
| 5 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若a1=12,a2=12+22+12,…,an=12+22+…+n2+…+22+12,在运用数学归纳法证明an=
n(2n2+1)时,第二步中从k到k+1应添加的项是( )
| 1 |
| 3 |
| A、k2+1 |
| B、(k2+1)2 |
| C、(k+1)2+k2 |
| D、(k+1)2+2k2 |
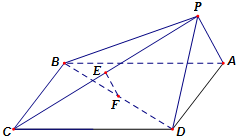 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.