题目内容
已知函数f(x)=lnx+
ax2-(a+1)x(a∈R).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的值;
(3)若对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+x1<f(x2)+x2恒成立,求a的取值范围.
| 1 |
| 2 |
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的值;
(3)若对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+x1<f(x2)+x2恒成立,求a的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)利用导数的几何意义可得切线的斜率f′(1),即可得到切线的方程;
(2)利用导数研究函数的单调性,再对a分类讨论即可得出;
(3)设g(x)=f(x)+x,则g(x)=lnx+
ax2-ax,由于对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+x1<f(x2)+x2恒成立,只要g(x)在(0,+∞)上单调递增即可.利用研究函数g(x)的单调性和对a分类讨论即可得出.
(2)利用导数研究函数的单调性,再对a分类讨论即可得出;
(3)设g(x)=f(x)+x,则g(x)=lnx+
| 1 |
| 2 |
解答:
解:(1)当a=1时,f(x)=lnx+
x2-2x,f′(x)=
+x-2.
∵f′(1)=0,f(1)=-
.
∴切线方程是y=-
.
(2)函数f(x)=lnx+
ax2-(a+1)x(a∈R)的定义域是(0,+∞).
当a>0时,f′(x)=
+ax-(a+1)=
=
.
令f′(x)=0,解得x=1或x=
.
当0<
≤1,即a≥1时,f(x)在[1,e]上单调递增,
∴f(x)在[1,e]上的最小值是f(1)=-
a-1=-2,解得a=2;
当1<
<e时,f(x)在[1,e]上的最小值是f(
),∴-lna-
-1=-2,即lna+
=1.
令h(a)=lna+
,h′(a)=
-
=
=0,可得a∈(
,
)函数h(a)单调递减,a∈(
,1)函数h(a)单调递增.
而h(
)=-1+
<1,不合题意.
当
≥e时,f(x)在[1,e]上单调递减,
∴f(x)在[1,e]上的最小值是f(e)=1+
ae2-(a+1)e=-2,解得a=
<0,不合题意.
综上可得:a=2.
(3)设g(x)=f(x)+x,则g(x)=lnx+
ax2-ax,
∵对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+x1<f(x2)+x2恒成立,
∴只要g(x)在(0,+∞)上单调递增即可.
而g′(x)=ax-a+
=
.
当a=0时,g′(x)=
>0,此时g(x)在(0,+∞)上单调递增;
当a≠0时,只需g′(x)≥0在(0,+∞)上恒成立,只要ax2-ax+1≥0,
则需要
,解得0<a≤4.
综上a的取值范围是:0≤a≤4.
| 1 |
| 2 |
| 1 |
| x |
∵f′(1)=0,f(1)=-
| 3 |
| 2 |
∴切线方程是y=-
| 3 |
| 2 |
(2)函数f(x)=lnx+
| 1 |
| 2 |
当a>0时,f′(x)=
| 1 |
| x |
| ax2-(a+1)x+1 |
| x |
| (x-1)(ax-1) |
| x |
令f′(x)=0,解得x=1或x=
| 1 |
| a |
当0<
| 1 |
| a |
∴f(x)在[1,e]上的最小值是f(1)=-
| 1 |
| 2 |
当1<
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2a |
| 1 |
| 2a |
令h(a)=lna+
| 1 |
| 2a |
| 1 |
| a |
| 1 |
| 2a2 |
| 2a-1 |
| 2a2 |
| 1 |
| e |
| 1 |
| 2 |
| 1 |
| 2 |
而h(
| 1 |
| e |
| e |
| 2 |
当
| 1 |
| a |
∴f(x)在[1,e]上的最小值是f(e)=1+
| 1 |
| 2 |
| 6-2e |
| 2e-e2 |
综上可得:a=2.
(3)设g(x)=f(x)+x,则g(x)=lnx+
| 1 |
| 2 |
∵对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+x1<f(x2)+x2恒成立,
∴只要g(x)在(0,+∞)上单调递增即可.
而g′(x)=ax-a+
| 1 |
| x |
| ax2-ax+1 |
| x |
当a=0时,g′(x)=
| 1 |
| x |
当a≠0时,只需g′(x)≥0在(0,+∞)上恒成立,只要ax2-ax+1≥0,
则需要
|
综上a的取值范围是:0≤a≤4.
点评:本题考查了利用导数研究函数的单调性极值与最值、导数的几何意义、切线的方程、二次函数与判别式的关系等基础知识与基本技能方法,考查了分类讨论的是幸福方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
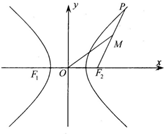 如图,双曲线
如图,双曲线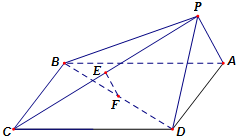 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD.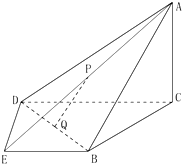 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=