题目内容
12.已知函数f(x)=1+$\frac{4}{x}$,g(x)=log2x;设函数h(x)=g(x)-f(x)求函数h(x)在区间[2,4]上的值域;
定义min{p,q}表示p,q中较小者,设函数H(x)=min{f(x),g(x)}(x>0)
①求函数H(x)的最大值;
②若函数y=H(x)-k有两个零点,求实数k的取值范围.
分析 (1)判断h(x)在区间[2,4]上单调递增,计算即可得到所求值域;
(2)①求出函数H(x)=min{f(x),g(x)}的分段函数,讨论单调性,可得最大值;
②若函数y=H(x)-k有两个零点等价于方程H(x)=k有两个实根;作出函数H(x)的大致图象,即可得到所求k的范围.
解答 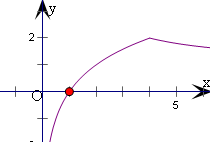 解:(1)因为函数h(x)=g(x)-f(x)=log2x-1-$\frac{4}{x}$
解:(1)因为函数h(x)=g(x)-f(x)=log2x-1-$\frac{4}{x}$
在区间[2,4]上单调递增,
所以函数h(x)的值域为[-2,0];-----------(4分)
(2)①函数H(x)=min{f(x),g(x)}=$\left\{\begin{array}{l}{lo{g}_{2}x,0<x≤4}\\{1+\frac{4}{x},x>4}\end{array}\right.$,
显然,函数H(x)在区间(0,4]上单调递增,在区间(4,+∞)上单调递减,
所以,函数H(x)的最大值为H(4)=2-------------(8分)
②若函数y=H(x)-k有两个零点等价于方程H(x)=k有两个实根;
作出函数H(x)的大致图象,可知k的取值范围是1<k<2-----------------(12分)
点评 本题考查函数的值域及最值的求法,注意运用函数的单调性和数形结合思想方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.函数f(x)=$\frac{\sqrt{2-x}}{{log}_{2}x}$的定义域为( )
| A. | {x|0<x≤2} | B. | {x|0<x≤2且x≠1} | C. | {x|0<x<2} | D. | {x|0<x<2且x≠1} |
4.在△ABC中,若A=60°,b=4,此三角形面积S=2$\sqrt{3}$,则a的值是( )
| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
1.已知f(x)=sinωx-cosωx(ω>$\frac{1}{4}$,x∈R),若f(x)的任何一条对称轴与x轴交点的横坐标都不属于区间(2π,3π),则ω的取值范围是( )
| A. | [$\frac{3}{8}$,$\frac{11}{12}$]∪[$\frac{11}{8}$,$\frac{19}{12}$] | B. | ($\frac{1}{4}$,$\frac{5}{12}$]∪[$\frac{5}{8}$,$\frac{3}{4}$] | ||
| C. | [$\frac{3}{8}$,$\frac{7}{12}$]∪[$\frac{7}{8}$,$\frac{11}{12}$] | D. | ($\frac{1}{4}$,$\frac{3}{4}$]∪[$\frac{9}{8}$,$\frac{17}{12}$] |
2.已知函数f(x+1)是定义在R上的奇函数,若对于任意给定的不等实数x1,x2不等式(x1-x2)[f(x1)-f(x2)]<0恒成立,则不等式f(2x-3)>0的解集为( )
| A. | (0,+∞) | B. | (1,+∞) | C. | (2,+∞) | D. | (-∞,2) |
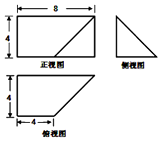 一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.
一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.