题目内容
已知对于任意实数m,不等式|5-3m|+|3m-4|≥x-
恒成立,则实数x的取值范围是 .
| 2 |
| x |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由绝对值三角不等式可得|5-3m|+|3m-4|≥=1,结合条件可得 1≥x-
恒成立,即
≤0,由此求得实数x的取值范围.
| 2 |
| x |
| (x+1)(x-2) |
| x |
解答:
解:由绝对值三角不等式可得|5-3m|+|3m-4|≥|5-3m+(3m-4)|=1,
又|5-3m|+|3m-4|≥x-
恒成立,
∴1≥x-
恒成立,
即
≤0,
解得x≤-1,或0<x≤2,
故答案为:(-∞,-1]∪(0,2].
又|5-3m|+|3m-4|≥x-
| 2 |
| x |
∴1≥x-
| 2 |
| x |
即
| (x+1)(x-2) |
| x |
解得x≤-1,或0<x≤2,
故答案为:(-∞,-1]∪(0,2].
点评:本题主要考查绝对值三角不等式,分式不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
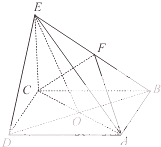 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点. 如图,圆O与△ABC的边AB,AC分别相切于点B,D,与BC边相交于点E,且∠BED=60°,AB=1,则圆O的半径长为
如图,圆O与△ABC的边AB,AC分别相切于点B,D,与BC边相交于点E,且∠BED=60°,AB=1,则圆O的半径长为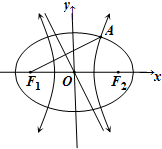 如图,F1,F2是椭圆C1:
如图,F1,F2是椭圆C1: