题目内容
过抛物线x2=
y的焦点作直线交抛物线于A、B两点,线段AB的中点M的纵坐标为2,则线段AB长为 .
| 1 |
| 8 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出准线方程为y=-
,由抛物线的定义可得AB=AA′+BB′,再由线段AB的中点M的纵坐标为2可得 2MM′=AA′+BB′,由此求得线段AB的长.
| 1 |
| 32 |
解答:
解:抛物线x2=
y中p=
.
设A、B、M在准线y=-
上的射影分别为A′、B′、M′,则由抛物线的定义可得AB=AA′+BB′.
再由线段AB的中点M的纵坐标为2可得 2MM′=AA′+BB′,即 2(2+
)=AA′+BB′=AB,
∴AB=
,
故答案为:
.
| 1 |
| 8 |
| 1 |
| 16 |
设A、B、M在准线y=-
| 1 |
| 32 |
再由线段AB的中点M的纵坐标为2可得 2MM′=AA′+BB′,即 2(2+
| 1 |
| 32 |
∴AB=
| 65 |
| 16 |
故答案为:
| 65 |
| 16 |
点评:本题主要考查抛物线的定义、标准方程,以及简单性质的应用,属于中档题.

练习册系列答案
相关题目
“若g′(x0)=0,则x0是函数y=g(x)的极值点,因为g(x)=x3中,g′(x)=3x2且g′(0)=0,所以0是g(x)=x3的极值点.”在此“三段论”中,下列说法正确的是( )
| A、推理过程错误 |
| B、大前提错误 |
| C、小前提错误 |
| D、大、小前提错误 |
用反证法证明命题“已知A,B,C,D是空间中的四点,直线AB与CD是异面直线,则直线AC和BD也是异面直线.”应假设( )
| A、直线AC和BD是平行直线 |
| B、直线AB和CD是平行直线 |
| C、直线AC和BD是共面直线 |
| D、直线AB和CD是共面直线 |
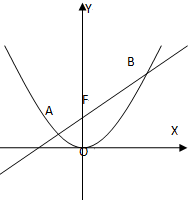 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.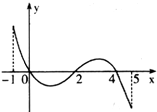 已知函数f(x)的定义域为[-1,5],部分对应值如图:
已知函数f(x)的定义域为[-1,5],部分对应值如图: